Project
EF1-19
Machine Learning Enhanced Filtering Methods for Inverse Problems
Project Heads
Claudia Schillings
Project Members
Philipp Wacker (until 09/22), Mattes Mollenhauer (02/23 until 02/24), Dana Wrischnig (from 05/24), Ilja Klebanov (from 05/24)
Project Duration
01.03.2022 − 31.12.2024
Located at
FU Berlin
Highlights
-
Convergence rates established for Sobolev-norm regularized operator learning in vector-valued settings [5, 6, 11]
-
Novel sub-Gaussian concentration inequalities for Hilbert space-valued random elements [10]
-
Deterministic sampling framework using transport-based formulations [9]
-
Enhanced ensemble Kalman inversion via control strategies [7]
-
Advanced cubature rules and quasi-Monte Carlo for Bayesian experimental design [4, 8]
Description
This project explores advanced machine learning-based filtering and inference techniques tailored to high-dimensional and infinite-dimensional inverse problems. At its core, the project seeks scalable, mathematically grounded algorithms for uncertainty quantification and Bayesian inference [15], with particular attention to ill-posed problems governed by PDEs.
The theoretical focus includes the statistical analysis of operator learning, deterministic sampling via transport maps, and concentration inequalities in infinite-dimensional settings. On the computational side, ensemble-based particle methods, control-augmented Ensemble Kalman inversion, and Bayesian design methods with advanced cubature techniques are developed and applied in complex scenarios.
The project leverages and extends ideas from Ensemble Kalman Filters (EnKF) [14] and Bayesian filtering, pushing toward new methods that integrate gradient information, deterministic transport, and data-efficient quadrature. These contributions provide robust and interpretable alternatives to black-box machine learning techniques in scientific computing.
Contributions
Learning Linear Operators in Hilbert Spaces [5, 6, 11]:
We investigate the learning of linear operators between Hilbert spaces, formulating it as a high-dimensional least-squares regression problem. Despite the non-compactness of the forward operator, we show equivalence with a compact inverse problem in scalar-valued regression. This allows us to derive dimension-free learning rates using tools from kernel regression and concentration of measure. These results form a theoretical foundation for scalable operator learning and uncertainty quantification.
Tail Behaviour of Subgaussian Vectors in Hilbert Spaces [10]:
We analyze the tail behaviour of norms and quadratic forms of sub-Gaussian random elements in Hilbert spaces. Using a trace-class operator to control moments, we establish new deviation bounds analogous to classical Hoeffding- and Bernstein-type inequalities. These insights are applied to derive robust variance estimates in regularized statistical inverse problems.
Bayesian Inference and Ensemble-Based Numerical Methods [3]:
We introduce ensemble-based gradient inference (EGI), a method to extract higher-order differential information from particle ensembles. This enhances sampling and optimization algorithms such as consensus-based optimization and Langevin dynamics. Numerical experiments demonstrate improved exploration of multimodal distributions. The implementation is available in this Github repository.
Spectral Regularization in Vector-Valued Learning [6]:
We extend classical spectral regularization methods to vector-valued regression using operator-valued kernels. We prove optimal convergence rates in Sobolev norms under general assumptions, advancing the theory of learning operators from data in infinite-dimensional settings.
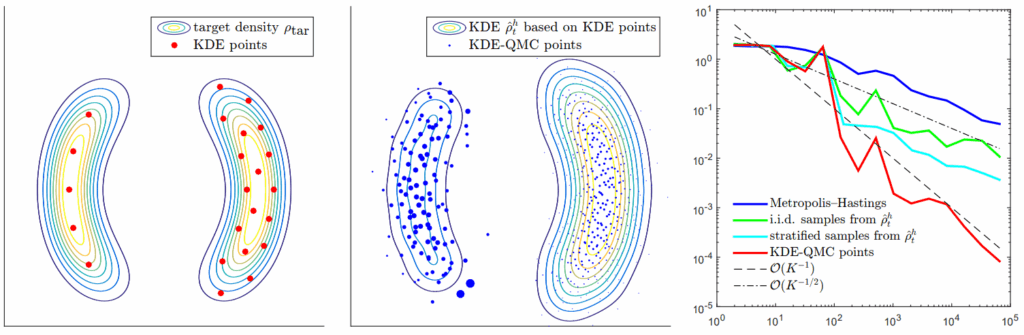
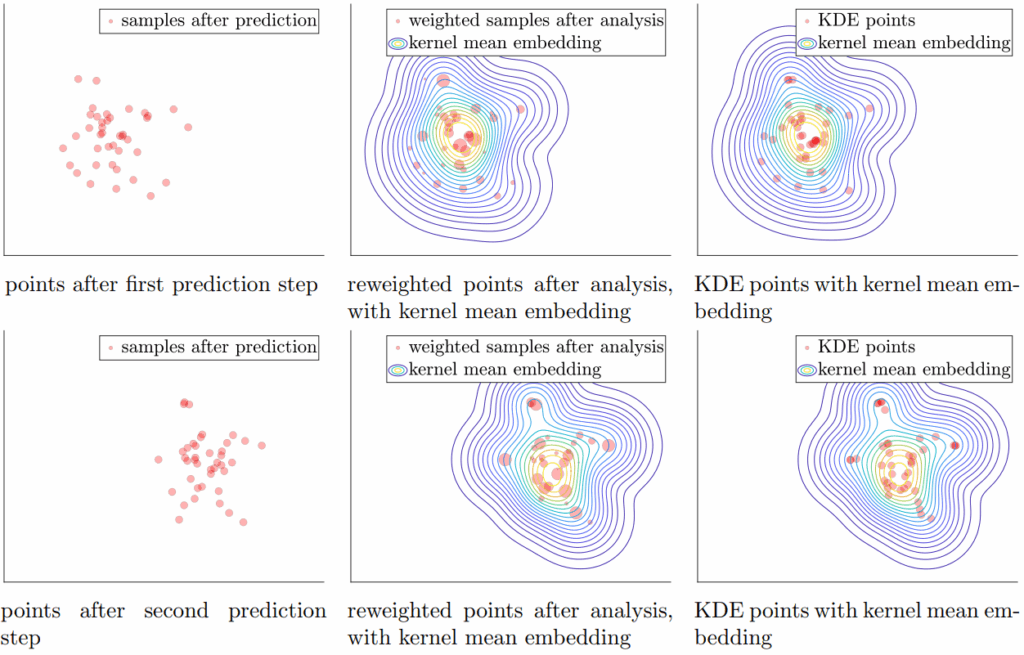
Deterministic Sampling via Transport [9]:
We propose a deterministic approach to sampling based on transport equations, particularly the Fokker–Planck framework. By avoiding random sampling noise, this method offers efficiency improvements in applications such as kernel mean embeddings, variational inference, and sequential Monte Carlo.
Control-Augmented Ensemble Kalman Inversion [7]:
We improve ensemble Kalman inversion by integrating ensemble control strategies. This extension enhances convergence stability and inference accuracy in ill-posed and high-dimensional inverse problems.
Quasi-Monte Carlo and Kernel Cubature for Bayesian Design [4, 8]:
We develop hybrid numerical integration techniques for Bayesian optimal experimental design governed by PDEs. Combining quasi-Monte Carlo lattice rules with kernel-based cubature, the resulting methods achieve high accuracy with fewer model evaluations.
Publications within project
Refereed Publications
[1] L. Bungert, T. Roith, and P. Wacker. Polarized consensus-based dynamics for optimization and sampling. Mathematical Programming, 2024.
[2] L. Bungert and P. Wacker. Complete deterministic dynamics and spectral decomposition of the linear ensemble Kalman inversion. SIAM/ASA Journal on Uncertainty Quantification, 11(1):320–357, 2023.
[3] C. Schillings, C. Totzeck, and P. Wacker. Ensemble-based gradient inference for particle methods in optimization and sampling. SIAM/ASA Journal on Uncertainty Quantification, 11(3):757–787, 2023.
[4] V. Kaarnioja, I. Klebanov, C. Schillings, and Y. Suzuki. Lattice rules meet kernel cubature, 2025. Accepted in MCMC Proceedings. arXiv:2501.09500.
[5] Z. Li, D. Meunier, M. Mollenhauer, and A. Gretton. Towards optimal Sobolev norm rates for the vector-valued regularized least-squares algorithm. Journal of Machine Learning Research, 25(181):1–51, 2024. Link
[6] D. Meunier, Z. Shen, M. Mollenhauer, A. Gretton, and Z. Li. Optimal rates for vector-valued spectral regularization learning algorithms. NeurIPS 2024. Link
Submitted Articles
[7] R. Harris and C. Schillings. Accuracy boost in ensemble Kalman inversion via ensemble control strategies, 2025. arXiv:2503.11308
[8] V. Kaarnioja and C. Schillings. Quasi-Monte Carlo for Bayesian design of experiment problems governed by parametric PDEs, 2024. arXiv:2405.03529
[9] I. Klebanov. Deterministic Fokker–Planck transport—with applications to sampling, variational inference, kernel mean embeddings & sequential Monte Carlo, 2024. arXiv:2410.18993
[10] M. Mollenhauer and C. Schillings. On the concentration of sub-Gaussian vectors and positive quadratic forms in Hilbert spaces, 2023. arXiv:2306.11404
[11] M. Mollenhauer, N. Mücke, and T. J. Sullivan. Learning linear operators: Infinite-dimensional regression as a well-behaved non-compact inverse problem. arXiv preprint, arXiv:2211.08875, 2022. arXiv:2211.08875
Student Theses
[12] L. Bazahica. Quasi-Monte Carlo integration for nonsmooth integrands. Master’s thesis, FU Berlin, 2023.
[13] S. Khanger. Adaptive sampling techniques: Comparative analysis of incremental mixture importance sampling and Metropolis-Hastings algorithms. Master’s thesis, FU Berlin, 2024.
Related Publications
[14] Blömker, D., Schillings, C., Wacker, P., & Weissmann, S. (2022). Continuous time limit of the stochastic ensemble Kalman inversion: Strong convergence analysis. SIAM Journal on Numerical Analysis, 60(6), 3181-3215.
[15] M. Dashti and A. M. Stuart (2017) The Bayesian approach to inverse problems. In Handbook of uncertainty quantification, Springer.
Related Pictures