Project
EF1-10
Kernel Ensemble Kalman Filter and Inference
Project Heads
Péter Koltai, Nicolas Perkowski
Project Members
Ilja Klebanov (until 24.10.2023), Marvin Lücke (from 01.07.2024)
Project Duration
01.04.2021 − 31.12.2024
Located at
FU Berlin
Description
We propose combining recent advances in the computation of conditional (posterior probability) distributions via Hilbert space embedding with the stochastic analysis of partially observed dynamical systems —exemplified by ensemble Kalman methods— to develop, analyse, and apply novel learning methods for profoundly nonlinear, multimodal problems.
Given a hidden Markov model, the task of filtering refers to the inference of the current hidden state from all observations up to that time. One of the most prominent filtering techniques is the so-called ensemble Kalman filter (EnKF), which approximates the filtering distribution by an ensemble of particles in the Monte Carlo sense.
While its prediction step is straightforward, the analysis or update step (i.e. the incorporation of the new observation via Bayes’ rule) is a rude approximation by the Gaussian conditioning formula, which is exact in the case of Gaussian distributions and linear models, but, in general, cannot be expected to reproduce the filtering distribution in the large ensemble size limit.
On the other hand, as we have found in our previous Math+ project (TrU-2), the Gaussian conditioning formula is exact for any random variables after embedding them into so-called reproducing kernel Hilbert spaces (RKHS), a methodology widely used by the machine learning community under the term “conditional mean embedding”.
Therefore, the question of how these two approaches can be combined arises quite naturally. The aim of this project is to eliminate the second source of error described above (in addition to the Monte Carlo error) by embedding the EnKF methodology into RKHSs. Further advantages of such an embedding is the potential to treat nonlinear state spaces such as curved manifolds or sets of images, graphs, strings etc., for which the conventional EnKF cannot even be formulated.
Contributions
Data assimilation, in particular filtering, is a specific class of Bayesian inverse problems in the context of partially observed dynamical systems. As such, several mathematical objects are of particular interest. These include point estimators of the posterior distributions, such as the conditional mean and the maximum a posteriori (MAP) estimator, as well as approximations of the posterior distribution itself.
Maximum a posteriori (MAP) estimators
Within this project, we have made several contributions to the definition, well-definedness and stability of MAP estimators [1,2,3,5].
While these estimators are widely used in practice and their definition is clear for continuous probability distributions over the Euclidean space, the corresponding concept in general (separable) metric spaces, in particular infinite-dimensional Banach and Hilbert spaces, typically occuring in the context of Bayesian inference for partial differential equations, is far less obvious, and several definitions have been suggested in the past — strong, weak and generalized modes. In [5], we analyze these and many further definitions in a structured way.
In addition to ambiguity of their definition, the existence of (strong and weak) MAP estimators is an open problem. It has been established for certain spaces in the case of Gaussian priors, and in [3] we improved on the state of the art in that regard.
Further, when it comes to practical applications, the stability of MAP estimators with respect to perturbations of the prior distribution, the likelihood model as well as the data plays a crucial role. In the twin papers [1,2] we establish an extensive analytical framework to address this problem.
Approximating posterior distributions
The central problem in Bayesian inference is the approximation of expected values with respect to a potentially complicated/multi-modal/high-dimensional target (posterior) distribution. If the dimension is high (roughly, larger than 5), classical quadrature rules suffer from the curse of dimensionality, which is why such targets are typically approximated by samples, that is, finitely many point masses.
While explicit formulas for direct (‘Monte-Carlo’) samples from the posterior are rarely available, several alternatives can be used, with Markov chain Monte Carlo methods and importance sampling being two of the most popular ones. All of these methods have a dimension-independent convergence rate, which, however, is rather slow. Importance sampling is often based on an importance distribution that is a mixture of simple distributions. In [6], we suggest to use higher-order quadrature rules (with better convergence rates, such as quasi-Monte Carlo and sparse grids) by establishing a transport map from a simple distribution to such a mixture, thereby extending the applicability of such quadrature rules to a wider class of probability distributions.
There is a direct application in data assimilation: The resampling step and prediction step within sequential Monte Carlo (SMC) correspond to sampling from a mixture distribution, which, thanks to our methodology, is now possible using higher-order cubature rules, e.g. QMC.
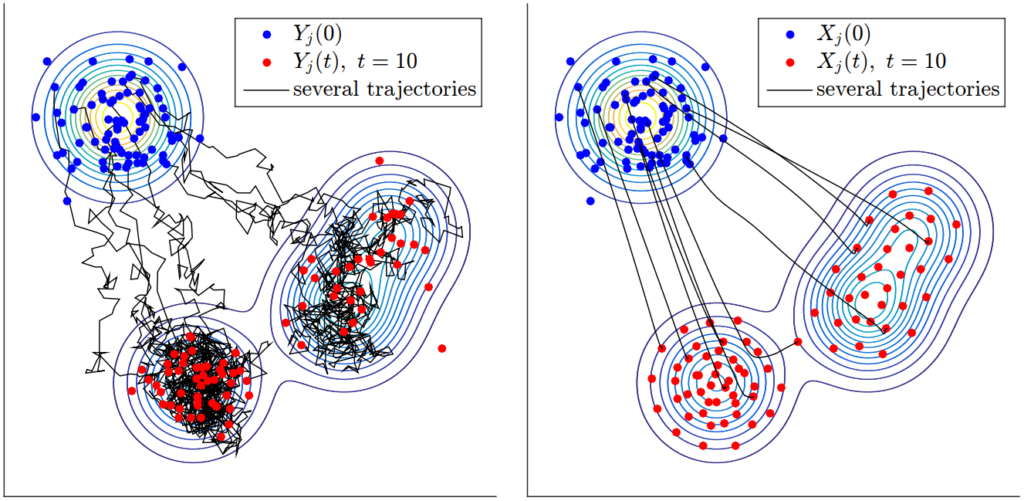
Deterministic Fokker-Planck transport and kernel mean outbeddings
Our recent work [7] explores the use of deterministic Fokker-Planck transport to approximate distributions via equal-weight mixtures of shifted kernels. This approach offers a principled and flexible method for representing complex distributions using tractable mixtures, constructed through a discretized version of the probability flow ODE associated with the Fokker-Planck equation.
A key application of this framework lies in kernel mean embeddings, particularly in enabling a novel procedure we refer to as kernel mean outbedding. In many settings, a conditional mean embedding provides an implicit representation of a conditional distribution. Recovering an explicit approximation of this conditional distribution requires a form of deconvolution — precisely the role played by our transport-based approach. By interpreting the transported kernel centers as samples from the deconvolved distribution, we enable efficient sampling and reconstruction from embedded distributions.
This procedure is not only well-suited for recovering explicit approximations from conditional mean embeddings, but is also of independent interest due to its broad applicability. The underlying transport framework extends naturally to tasks such as sampling, variational inference, and sequential Monte Carlo, where its deterministic structure supports accurate approximations via high-order cubature rules and importance reweighting.
Publications within Project
- [1] Birzhan Ayanbayev, IK, Han Cheng Lie, Tim Sullivan, Γ-convergence of Onsager-Machlup functionals. Part I: With applications to maximum a posteriori estimation in Bayesian inverse problems, 2021 [Inverse Problems] [arxiv]
- [2] Birzhan Ayanbayev, IK, Han Cheng Lie, Tim Sullivan, Γ-convergence of Onsager-Machlup functionals. Part II: Infinite product measures on Banach spaces, 2021 [Inverse Problems] [arxiv]
- [3] Ilja Klebanov, Philipp Wacker, Maximum a posteriori estimators in ℓ^p are well-defined for diagonal Gaussian priors, 2023 [Inverse Problems] [arxiv]
- [4] Ilja Klebanov, Graph convex hull bounds as generalized Jensen inequalities, 2023 [BLMS] [arxiv]
- [5] Ilja Klebanov, Hefin Lambley, Tim Sullivan, Classification of small-ball modes and maximum a posteriori estimators, 2025 [arxiv]
- [6] Ilja Klebanov, Tim Sullivan, Transporting Higher-Order Quadrature Rules: Quasi-Monte Carlo Points and Sparse Grids for Mixture Distributions, 2023 [arxiv]
- [7] Ilja Klebanov, Deterministic Fokker-Planck Transport – With Applications to Sampling, Variational Inference, Kernel Mean Embeddings & Sequential Monte Carlo, 2024 [arxiv]
- [8] M. Mollenhauer, S. Klus, Ch. Schütte, and P. Koltai, Kernel autocovariance operators of stationary processes: estimation and convergence, 2022. [JMLR]
- [9] A. Bittracher, S. Klus, B. Hamzi, P. Koltai, and Ch. Schütte, Dimensionality Reduction of Complex Metastable Systems via Kernel Embeddings of Transition Manifolds, 2021, DOI: 10.1007/s00332-020-09668-z [Journal of Nonlinear Science]
- [10] R. Polzin, I. Klebanov, N. Nüsken, P. Koltai, Coherent set identification via direct low rank maximum likelihood estimation, 2023 [arxiv]
Related Publications
- I. Klebanov, I. Schuster, and T. J. Sullivan. A rigorous theory of conditional mean embeddings. SIAM J. Math. Data Sci., 2020.
- M. Mollenhauer, S. Klus, C. Schütte, and P. Koltai. Kernel autocovariance operators of stationary processes: Estimation and convergence, 2020. arXiv:2004.00891.
- I. Schuster, M. Mollenhauer, S. Klus, and K. Muandet. Kernel conditional density operators. In Proceedings of the 23rd AISTATS 2020, Proceedings of Machine Learning Research, 2020.
- H. C. Yeong, R. T. Beeson, N. S. Namachchivaya, and N. Perkowski. Particle filters with nudging in multiscale chaotic systems: With application to the Lorenz ’96 atmospheric model. J. Nonlinear Sci., 30(4):1519-1552, 2020.
- A. Bittracher, S. Klus, B. Hamzi, P. Koltai, and C. Schütte. Dimensionality reduction of complex metastable systems via kernel embeddings of transition manifolds, 2019. arXiv:1904.08622.
- N. B. Kovachki and A. M. Stuart. Ensemble Kalman inversion: a derivative-free technique for machine learning tasks. Inverse Probl., 35(9):095005, 35, 2019.
- J. Diehl, M. Gubinelli, and N. Perkowski. The Kardar-Parisi-Zhang equation as scaling limit of weakly asymmetric interacting Brownian motions. Comm. Math. Phys., 354(2):549-589, 2017.
- C. Schillings and A. M. Stuart. Analysis of the ensemble Kalman filter for inverse problems. SIAM J. Numer. Anal., 55(3):1264-1290, 2017.
- O. G. Ernst, B. Sprungk, and H.-J. Starkloff. Analysis of the ensemble and polynomial chaos Kalman filters in Bayesian inverse problems. SIAM/ASA J. Uncertain. Quantif., 3(1):823-851, 2015.
- K. Fukumizu, L. Song, and A. Gretton. Kernel Bayes’ rule: Bayesian inference with positive definite kernels. J. Mach. Learn. Res., 14(1):3753-3783, 2013.
- P. Imkeller, N. S. Namachchivaya, N. Perkowski, and H. C. Yeong. Dimensional reduction in nonlinear filtering: A homogenization approach. Ann. Appl. Probab., 23(6):2290-2326, 2013.
- M. Goldstein and D. Wooff. Bayes Linear Statistics: Theory and Methods. Wiley Series in Probability and Statistics. John Wiley & Sons, Ltd., Chichester, 2007.
- G. Evensen. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans, 99(C5):10143-10162, 1994.
Related Picture 1

Related Picture 2
Related Picture 3

Related Picture 4


