AA5 – Variational Problems in Data-Driven Applications

Project

AA5-4 (was EF1-22)

Bayesian Optimization and Inference for Deep Networks

Project Heads

Claudia Schillings, Vladimir Spokoiny

Project Members

Oleg Butkovsky

Project Duration

01.01.2023 − 31.12.2024

Located at

WIAS

Description

Uncertainty quantification (UQ) and reliability of deep neuronal networks is an important research question. This project aims at developing of novel numerically efficient methods for inference and UQ analysis of DNN with theoretical guarantees. Particular issues to address are high parameter dimension and nonconvexity of the objective function. We propose a new insight on the problem using the recent progress in high dimensional Laplace approximation. A further goal is to apply the proposed methods to various application problems.

External Website

Selected Publications

- S. Athreya, O. Butkovsky, K. Lê, L. Mytnik. Well-posedness of stochastic heat equation with distributional drift and skew stochastic heat equation. Communications on Pure and Applied Mathematics, 77, 2708–2777, 2024.
- C. Bayer, D. Belomestny, O. Butkovsky, J. Schoenmakers. RKHS regularization of singular local stochastic volatility McKean-Vlasov models. Finance and Stochastics, 28, 1147–1178, 2024.
- O. Butkovsky, K. Lê, L. Mytnik. Stochastic equations with singular drift driven by fractional Brownian motion. Probability and Mathematical Physics, 6-3, 857-912, 2025.
- O. Butkovsky, K. Dareiotis, M. Gerencsér. Strong rate of convergence of the Euler scheme for SDEs with irregular drift driven by Lévy noise. Annales de l’Institut Henri Poincare (B) Probabilites et Statistiques, to appear, 2025+, arXiv:2204.12926.
- O. Butkovsky, S. Gallay. Weak existence for SDEs with singular drifts and fractional Brownian or Levy noise beyond the subcritical regime, 2023, arXiv:2311.12013.
- O. Butkovsky, L. Mytnik. Weak uniqueness for singular stochastic equations, 2024, arXiv:2405.13780.
- S. Athreya, O. Butkovsky, K. Lê, L. Mytnik (2024). Analytically weak and mild solutions to stochastic heat equation with irregular drift. arXiv:2410.06599.

Related Pictures

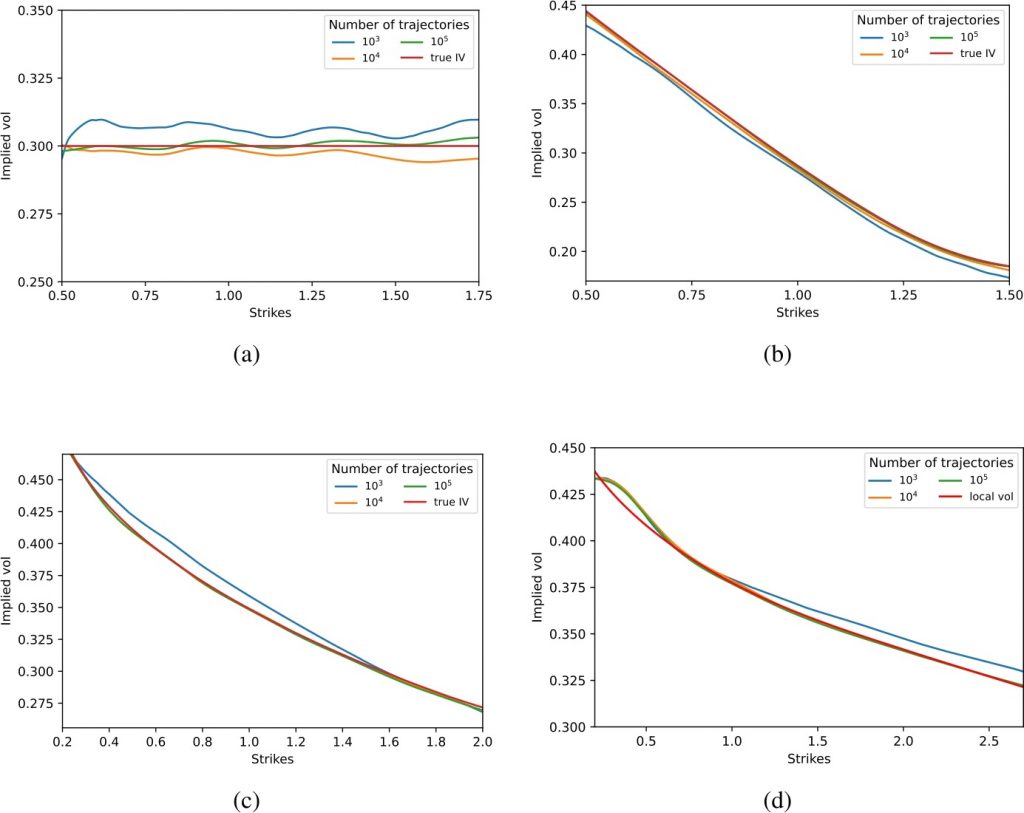
Fit of the smile for different number of particles: (a) Black–Scholes setting, T=1 $T = 1$ year; (b) Heston setting, T=1 $T = 1$ year; (c) Heston setting, T=4 $T = 4$ years; and (d) Heston setting, T=10 $T = 10$ years

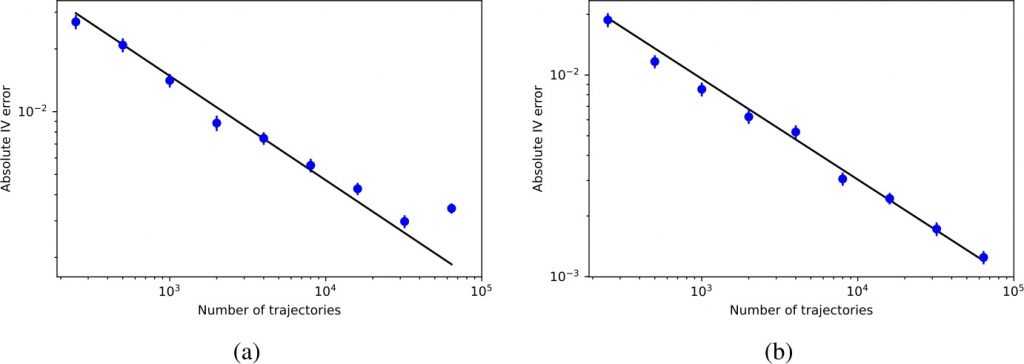
Mean absolute implied volatility error versus number of trajectories. The black line is the approximation: error = CN^-1/2; (a) Black–Scholes setting, C=0.469 $C = 0.469$ ; (b) Heston setting, C=0.303 $C = 0.303$