Project
AA5-10
Robust Data-Driven Reduced-Order Models for Cardiovascular Imaging of Turbulent Flows
Project Heads
Alfonso Caiazzo, Jia-Jie Zhu, Leonid Goubergrits
Project Members
Sarah Katz
Collaborators
Francesco Romor (WIAS), Felipe Galarce (PUCV, Valparaiso, Chile), Damiano Lombardi (INRIA, Paris)
Project Duration
01.10.2024 − 30.09.2026
Located at
WIAS
Description
Cardiovascular imaging supports physicians in staging the severity of cardiovascular diseases non-invasively and in monitoring postoperative progress. For coarctation of the aorta (CoA), a congenital heart defect with a localized narrowing in the aorta, image-based diagnosis relies on measuring patient anatomy, blood velocities, and ow rates in the narrowed area, to identify abnormal ow conditions and increased pressure gradient across the narrowing.
Due to the limited spatial resolution, MRI and echocardiography images do not allow to measure these quantities directly. Computed tomography (CT) scans can provide higher details, but they require radiation exposure and the use of contrast agents. Blood flow simulations play therefore an important role to obtain quantitative estimation of relevant biomarkers using limited measurements.
This project focuses on data assimilation based on a parametrized background data-weak (PBDW) method. This approach seeks a reconstruction of the numerical solution of a target PDE from limited measurements by minimizing the discrepancy between the reconstructed solution and a physics-informed reduced-order model (ROM), i.e., a subspace spanned by solutions of the target PDE. One main limitation of this method is that it relies on linear reduced-order subspaces (constructed, e.g., via proper orthogonal decomposition (POD). In the context of coarctation, turbulence modeling plays a relevant role and it is well known that linear ROMs are no longer suitable for building efficient and accurate approximations of the fluid dynamics.
To robustly support the cardiovascular imaging of turbulent flows, this project aims at designing and implementing new data assimilation methods combining linear reduced-order modeling and non-linear data-driven components.
The first goal will be the robust extension of the PBDW data assimilation taking into account physics-informed subspaces built from numerical simulations on different shapes. The second goal of the project will be to extend the PDBW with active learning. The third goal will be to derive learning-theoretical generalizations to enable further applications of digital shapes linked to shape optimization problems.
External Website
Project Publications
F. Romor, F. Galarce, J. Brüning, L. Goubergrits, A. Caiazzo.
Data assimilation performed with robust shape registration and graph neural networks: application to aortic coarctation
arxiv preprint 2502.12097 (2025) – submitted
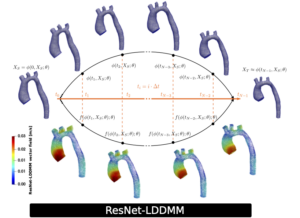
Abstract Computational hemodynamics can enhance image-based diagnostic and provide complementary insights to predict, understand, and monitor treatments. The high computational costs and the complexity associated with handling patient-specific settings still remain a major challenge towards clinical applications. In this work, we propose a robust shape registration method for aortic geometries. The approach is based on ResNet-LDDMM trained with a dataset of real and synthetic shapes. The optimization is tailored to surface meshes, and combined with a multigrid strategy to handle realistic mesh sizes. The registration allows to define geometric encodings of different blood flow solutions on a single reference shape, as well as to build projection-based reduced-order models. We employ this geometrical encoding to improve the training of encode-process-decode graph neural networks and present potential applications in data assimilation problems, combined with a generalized Parametrized-Background Data-Weak formulation. We address the reconstruction of velocity fields and wall shear stresses, as well as the estimation of pressure fields and pressure-related biomarkers, like the pressure drop, from low-resolution velocity observations. We show different numerical tests based on the synthetic data, comparing the proposed strategies with state of the art estimators.
Conferences & News
- [upcoming] ENUMATH 2025, Heidelberg
- 23rd IACM Computational Fluid Conference (CFC) 2025, Santiago (Chile)
- Numerical Methods in Applied Mathematics (MESIGA 2025), Potsdam
- 3rd Digital Twins in Engineering (DTE AIECCOMAS) Conference 2025, Paris
- 8th Int. Conference on Computational and Biomedical Engineering (CompBioMed ) 2024,George Mason University, Arlington (USA)
Selected Pictures
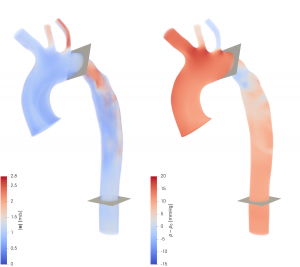
Simulation of aortic flow (Left: velocity field, Right: pressure field)

Set of geometries which can be registered to a reference patient (in orange)

