Project
AA4-5
Energy-Based Modeling, Simulation, and Optimization of Power Systems under Uncertainty
Project Heads
Volker Mehrmann, Caren Tischendorf, Matthias Voigt
Project Members
Lena Scholz (TU)
Project Duration
01.01.2019 – 31.12.2021
Located at
TU Berlin
Description
Modern power systems need to be controlled and optimized as dynamical systems in real time, rather than as stationary systems as is the case today. To properly deal with strong decentralization, new long distance DC transmission lines, and the increased randomness in power generation, a complete model hierarchies of different modeling granularity should be set up that can be used for different simulation, control, and optimization tasks. As basis we use energy-based models (or port-Hamiltonian systems) of (partial) differential-algebraic equations that also allow the appropriate treatment of stochasticity and time-delay.
Within the project a new port-Hamiltonian formulation of power systems has been constructed that has many improved properties. The new compact port-Hamiltonian form derived in [Nedialkov, Pryce & Scholz 2021] has remarkable simplicity and symmetry, is proven to be always structurally amenable, and gives rise to a differential-algebraic equation system that always has an index at most 1. Moreover, the modeling framework of port-Hamiltonian descriptor systems has been extended to include under- and over-determined systems and arbitrary differentiable Hamiltonian functions [Mehrmann & Morandin 2019].
Project Webpages
Selected Publications
- V. Mehrmann and P. Van Dooren: Optimal robustness of passive discrete-time systems. IMA Journal of Mathematical Control and Information, 37(4):1248-1269, 2020. (http://arxiv.org/abs/1909.06871)
- K. Cherifi, V. Mehrmann, and K. Hariche: Numerical methods to compute a minimal realization of a port-Hamiltonian system. Preprint 08-2019, Institute of Mathematics, TU Berlin, 2019. (http://arxiv.org/abs/1903.07042)
- L. Scholz: Condensed forms for linear port-Hamiltonian descriptor systems. Electronic Journal of Linear Algebra, 35: 65-89, 2019.
- C. Mehl, V. Mehrmann, and M. Wojtylak: Distance problems for dissipative Hamiltonian systems and related matrix polynomials. Linear Algebra and its Applications, 623:335-366, 2021. (http://arxiv.org/abs/2001.08902)
- C. A. Beattie, S. Gugercin and V. Mehrmann: Structure-preserving Interpolatory Model Reduction for Port-Hamiltonian Differential-Algebraic Systems. Festschrift to honor the 70th birthday of A. Antoulas, 2020. (http://arxiv.org/abs/1910.05674)
- V. Mehrmann and R. Morandin: Structure-preserving discretization for port-Hamiltonian descriptor systems. Proceedings of the 58th IEEE Conference on Decision and Control (CDC), 9.-12.12.19, Nice, pp. 6863-6868, 2019. (http://arxiv.org/abs/1903.10451)
- D. Bankmann, V. Mehrmann, Y. Nesterov, and P. Van Dooren: Computation of the analytic center of the solution set of the linear matrix inequality arising in continuous- and discrete-time passivity analysis. Vietnam Journal of Mathematics, 48(4):1-27, 2020. (http://arxiv.org/abs/1904.08202)
- N. Nedialkov, J.D. Pryce and L. Scholz: An Energy-based, always Index <= 1 and Structurally Amenable Electrical Circuit Model. Submitted for publication, 2021. (https://arxiv.org/abs/2108.05106).
- D. Hinsen: A Port-Hamiltonian Approach for the Modeling of Power Networks including the Telegraph Equations. Master thesis, TU Berlin, October 2020.
- A. Gonzalez-Zumba and P. Fernandez-de-Cordoba and J. Cortes and V. Mehrmann: Stability Assessment of Stochastic Differential-Algebraic Systems via Lyapunov Exponents with an Application to Power Systems. Mathematics, 8(9):1393, 2020.
- P. Schwerdtner and M. Voigt: SOBMOR: Structured optimization-based model order reduction. Revision submitted for publication, 2021. (https://arxiv.org/abs/2011.07567)
- P. Schwerdtner and M. Voigt: Adaptive sampling for structure-preserving model order reduction of port-Hamiltonian systems. IFAC-PapersOnLine, 54(19):143-148, 2021.
- V. Mehrmann and B. Unger: Control of port-Hamiltonian differential-algebraic systems and applications, Invited survey in Acta Numerica, to appear in 2022. (https://arxiv.org/abs/2201.06590)
- S. Bäse: Time-Limited Balanced Truncation Model Order Reduction for Descriptor Systems, Master thesis, TU Berlin, July 2021.
Selected Pictures

A simple DC power network
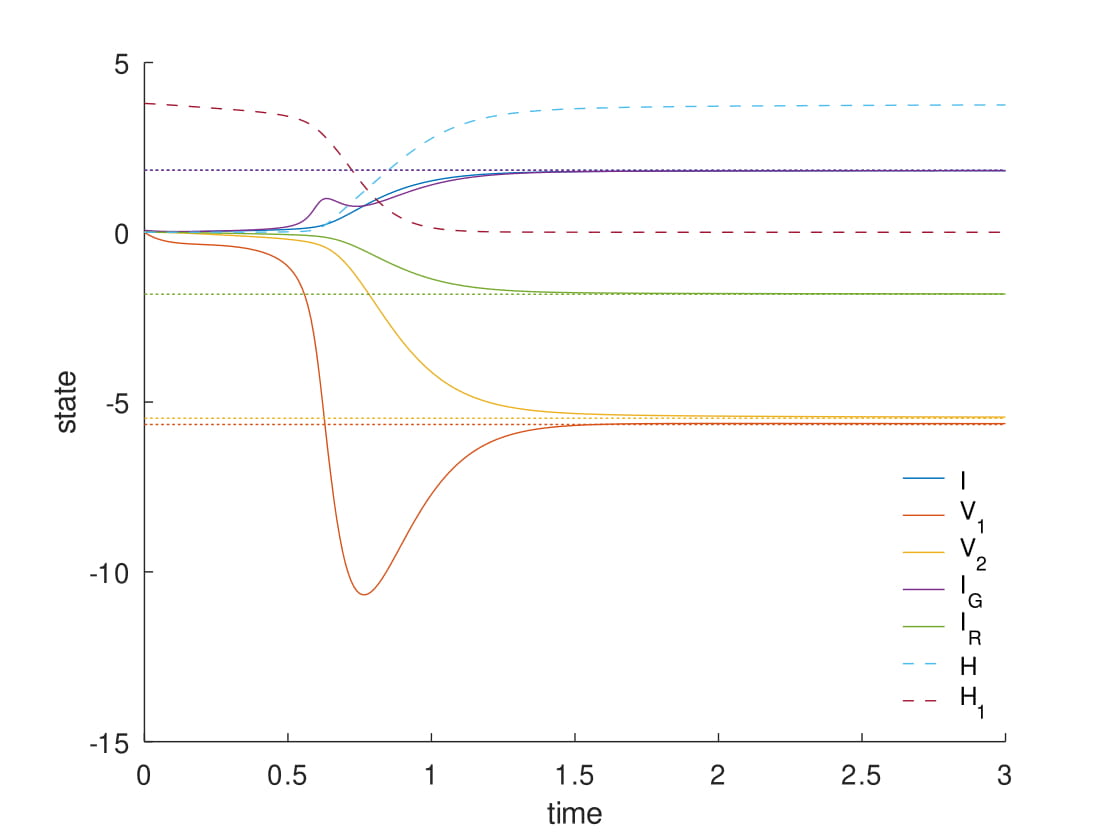
Evolution of the states of a controlled port-Hamiltonian power system model
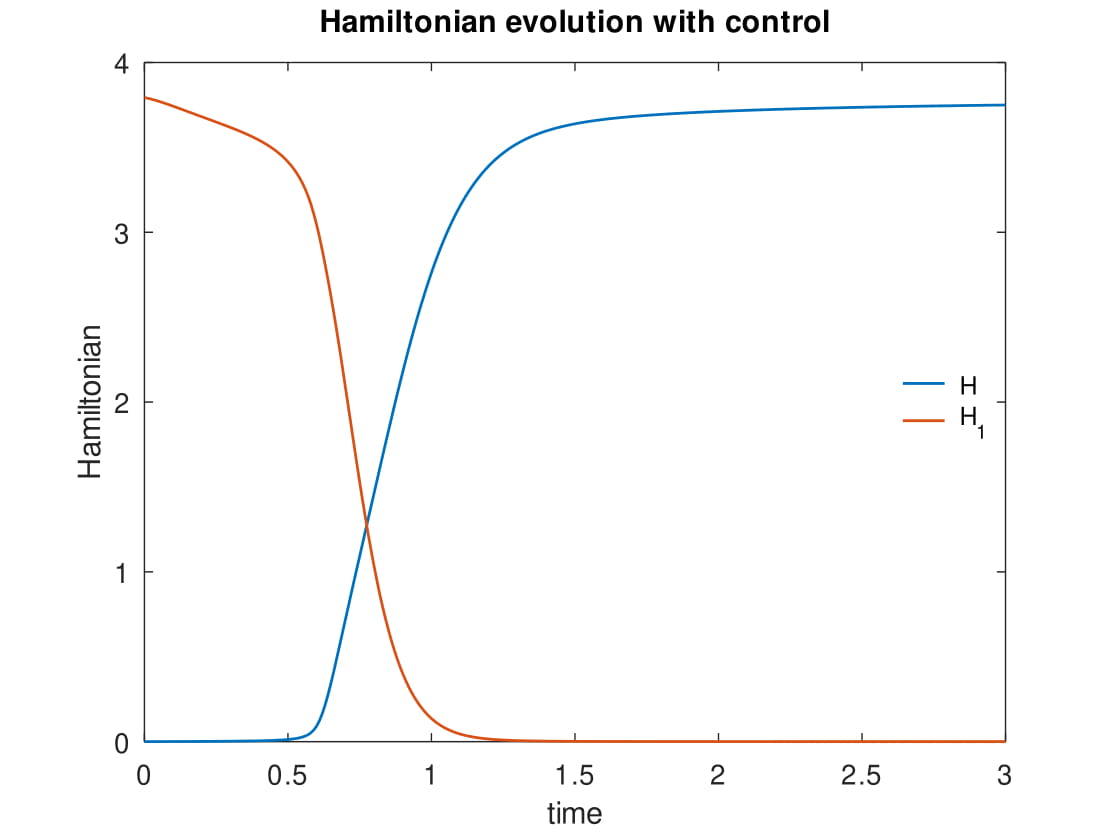
Evolution of the Hamiltonian of a controlled port-Hamiltonian power system model
Please insert any kind of pictures (photos, diagramms, simulations, graphics) related to the project in the above right field (Image with Text), by choosing the green plus image on top of the text editor. (You will be directed to the media library where you can add new files.)
(We need pictures for a lot of purposes in different contexts, like posters, scientific reports, flyers, website,…
Please upload pictures that might be just nice to look at, illustrate, explain or summarize your work.)
As Title in the above form please add a copyright.
And please give a short description of the picture and the context in the above textbox.
Don’t forget to press the “Save changes” button at the bottom of the box.
If you want to add more pictures, please use the “clone”-button at the right top of the above grey box.

