Project
AA4-4
Stochastic Modeling of Intraday Electricity Markets
Project Heads
Dörte Kreher, Markus Reiß
Project Members
Cassandra Milbradt (HU)
Project Duration
15.04.2019 – 14.04.2022
Located at
HU Berlin
Description
This project aims at developing (in-)finite dimensional, stochastic models for intraday electricity markets with continuous trading, with a special focus on the newly launched integrated European intraday electricity market “Singe Intraday Coupling” (short SIDC, formerly known as XBID market). Starting from a microscopic description of the market model, we derive heavy traffic approximations of the system dynamics yielding a tractable description of the volumes, prices, and available transmission capacities via stochastic (partial) differential equations.
As opposed to the existing structural energy market models, we develop analytically tractable, mathematical models for intraday electricity markets based on their observable market microstructure and therefore on statistically measurable input factors. This may presumably be useful to gain not only qualitative, but also quantitative insights into the German Intraday Electricity Market as well as the SIDC market project.
Project 1 – Jump diffusion approximation for the price dynamics of a fully state dependent limit order book model (cf. Preprint [arXiv], finished Nov 2020):
Intraday electricity markets with a continuous trading mechanism are known to be quite illiquid yielding particularly frequent extreme price movements over short time periods. The inclusion of large price jumps is therefore essential if one wants to approximate the price dynamics of intraday electricity markets with continuous trading. For this reason, we establish an approximation of the prices in limit order book dynamics by jump diffusion processes in the scaling limit. While conditions to derive limit theorems toward diffusion processes are generally well-understood, to the best of our knowledge this is not true for a jump diffusion limit. The main novelty is therefore to come up with a new set of assumptions that allows for a jump diffusion approximation of the prices in the scaling limit. Our derived limit order book approximation allows for a quite general dependence structure, where all coefficient functions are allowed to depend on current prices, standing volumes, and time.
Project 2 – A cross-border market model with limited transmission capacities (cf. Preprint [arXiv], finished July 2022):
In the SIDC, market participants of different countries are allowed to trade with each other on a cross-border basis. The total number of cross-border trades is, however, limited through the available transmission capacities. If all capacities are occupied, market orders can only be matched with standing volumes of the same origin. Motivated by the SIDC market dynamics, we derive a simple queuing system of the microscopic market dynamics between two countries based on limit order books. In order to take the limitation of transmission capacities into account, it turns out to be crucial to keep track of the origin of each incoming market and limit order and to count the number of executed cross-border trades over time. The latter is done by introducing a so-called capacity process to the market dynamics. After incorporating appropriate high-frequency assumptions to the microscopic model, we study its scaling behavior toward a continuous-time limit process. In the high-frequency limit, the cross-border market dynamics is described by a continuous-time regime switching process that alternates between regimes in which cross-border trading is allowed and regimes in which incoming market orders can only be matched with standing volumes of the same origin.
The two models derived in Project 1 and 2 follow fundamentally different approaches and the merging of them into a joint analytically tractable model is anything but trivial. Nevertheless, both models are interesting from a practitioner’s point of view. For application purposes, neither model is generally preferable to the other, and the selection of the appropriate model depends on the underlying problem and available data.
Project 3 – Parametric change point detection with random occurrence of the change point (cf. Preprint [arXiv], finished July 2022):
Calibration of mathematical models is one of the main concerns form a practitioner’s point of view. It is well known that change points (abrupt variations) are present in high-frequency financial data. If they are endogenously caused (e.g. by the total occupation of transmission capacities in the SIDC market), the dependence on the underlying data must be considered when estimating such change points. The existing theory on change point detection in parametric models is extended such that even random change points, depending on the data, can be handled by already known test statistics and estimators for the location and size of change points.
Selected Publications
- D. Kreher and C. Milbradt. Jump diffusion approximation for the price dynamics of a fully state dependent limit order book model. 2021. Preprint. Available at [arXiv]. Submitted to SIAM Journal of Financial Mathematics.
- C. Milbradt. A cross-border market model with limited transmission capacities. 2022. Preprint. Available at [arXiv].
- C. Milbradt. Parametric change point detection with random occurrence of the change point. 2022. Preprint. Available at [arXiv].
Selected Pictures
Simulation of the cross-border market model between two countries with limited transmission capacities (cf. Project 2): Best bid queues (top left), best ask queues (top right), best bid price dynamics of country F (orange) and country G (turkoise) (bottom left), and capacity dynamics (bottom right). Dependent of the state of the capacity process, we observe two different regimes in which cross-border trading is allowed (white) or prohibited (gray).
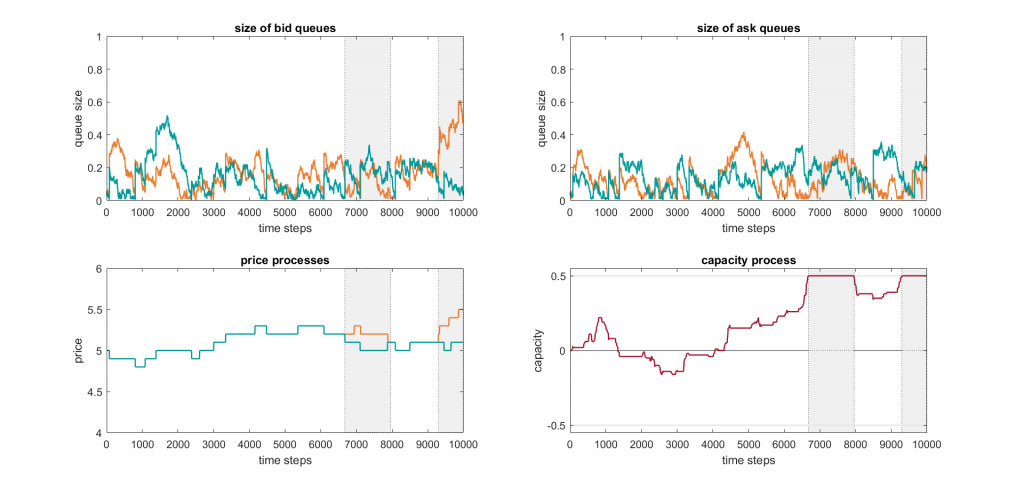
Cross-border market model with limited transmission
Simulation the limit order book dynamics of a single contract in a national limit order book (cf. Project 1): Evolution of the best bid and ask prices and the standing volumes at the bid and ask side in absolute coordinates.
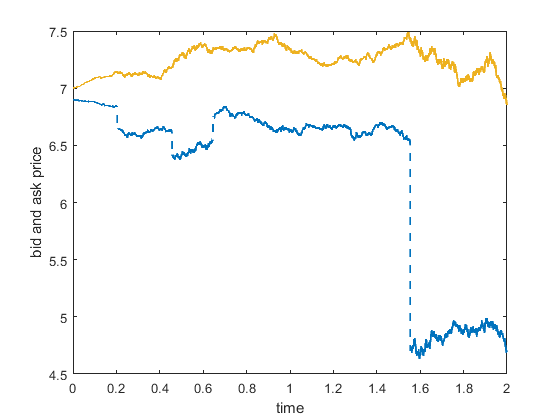
Best bid (blue) and ask (yellow) prices

Standing volumes at the bid side in absolute coordinates
Standing volumes at the ask side in absolute coordinates
Please insert any kind of pictures (photos, diagramms, simulations, graphics) related to the project in the above right field (Image with Text), by choosing the green plus image on top of the text editor. (You will be directed to the media library where you can add new files.)
(We need pictures for a lot of purposes in different contexts, like posters, scientific reports, flyers, website,…
Please upload pictures that might be just nice to look at, illustrate, explain or summarize your work.)
As Title in the above form please add a copyright.
And please give a short description of the picture and the context in the above textbox.
Don’t forget to press the “Save changes” button at the bottom of the box.
If you want to add more pictures, please use the “clone”-button at the right top of the above grey box.

