Project
AA3-9
Information Design for Bayesian Networks
Project Heads
Max Klimm
Project Members
Svenja M. Griesbach
Project Duration
01.10.2021 − 30.09.2024
Located at
TU Berlin
Description
This project studies information revelation and information exploitation in networks.
For the former, we consider traffic networks where a principal has full knowledge of the state of a system while the system users only have prior information about the state. We obtain characterizations of networks for which it is always optimal to reveal the information about the realized state to the system users and devise algorithms for the (approximate) computation of optimal signaling schemes.
For the information retrieval problem, we consider a network where a treasure is hidden at a vertex. We only know the probability that the treasure is hidden at a vertex, and we are interested in computing in which order the edges should be constructed so that the expected time until the treasure is found is minimized.
Information Revelation
The selfish behavior of network users degrades the performance of traffic networks. A popular model to study these effects is the static traffic model of Wardrop. Here, the road network is modeled as a directed graph where each edge of the graph corresponds to a road segment. The travel times in the graph are modeled as cost functions on the edges where the cost of an edge is a function of the total flow on that edge.
In this project, we study a generalization of the model where the travel time of each edge also depends on a state of the world θ ∈ Θ that is unknown to the traffic participants. However, the traffic participants share a common belief regarding the state of the world. The state θ may model certain weather or traffic scenarios in real-world traffic networks. We put ourselves in the shoes of a benevolent mediator who knows the true state of the world before any flow is routed. In real-world networks, this may correspond to a traffic service provider observing real-time traffic data.
The mediator may now strategically reveal information regarding the true state of the world to induce a good traffic equilibrium, i.e., an equilibrium with a low overall travel time.
In this project, we study the mathematical problem of computing the optimal information structures that induce the best-possible equilibria in these settings.
Let us first illustrate the concepts and the problem in the following simple example which is also illustrated in Figure 1.
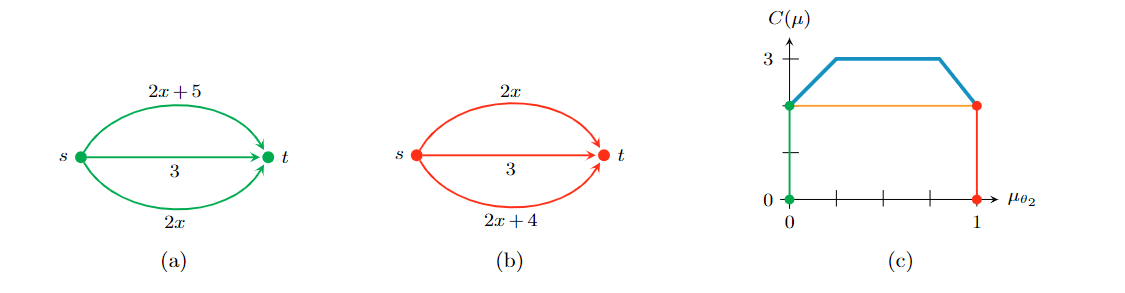
There are two vertices V = {s, t} and three parallel edges between s and t. There are two states θ1 and θ2. There is a single commodity with a volume of 1. The cost functions are given in Figure 1. We analyze the Wardrop equilibrium for all distributions μ ∈ Δ(Θ), where μ ∈ Δ(Θ) is interpreted as the unit interval for μ2 = 1 – μ2 ∈ [0,1]. For μ2 ∈ [0, 1/4], the equilibrium only uses the lowest edge, since the total cost for a volume of 1 is at most 3, whereas both other edges have an offset of at least 3. For μ2 ∈ [1/4, 2/5], the equilibrium uses only the two lower edges, since the upper edge has an offset of at least 3. The equilibrium uses all three edges for μ2 ∈ [2/5, 3/4]. Then, for μ2 ∈ [3/4, 4/5], the equilibrium uses only the two upper edges, since the offset of the lowest edge is at least three and therefore too high. Finally, for μ2 ∈ [4/5, 1], only the upper edge is used. Figure 1 shows the cost C(μ) of the resulting Wardrop equilibrium for all μ ∈ Δ(Θ) in blue. The function C(μ) is piecewise linear and concave over Δ(Θ). A signaling scheme Φ is a convex decomposition of μ into distributions μ(σ) ∈ Δ(Θ), and C(Φ) is a convex combination of C(μ(σ)). Since the cost is concave over Δ(Θ), we know that C(μ2) ≥ μ2 C(1) + (1 – μ2) C(0) for all μ2 ∈ [0, 1] as indicated by the orange function in Figure 1. This shows that, instead of mixing states into a signal with some interior distribution μ2 ∈ (0, 1), we rather want to send signals with μ2 ∈ {0, 1} that fully reveal the information about the state of nature. This can only improve the overall cost of C(Φ). Therefore, there is an optimal signaling scheme in which the principal sends an exclusive signal σ for each state Θ.
In Griesbach et al. [1], we show that full information revelation is in fact always optimal when the underlying network is series-parallel and the costs are affine with state-dependent offset. This characterization is tight in the sense that for every graph that is not series-parallel, there are cost functions such that full information revelation is not optimal.
We further show that the problem of computing the optimal signaling scheme can be reduced to the problem of computing all supports of Wardrop equilibria that appear for some beliefs. A computational study further reveals that the number of supports that appear for different beliefs is usually small on realistic instances.
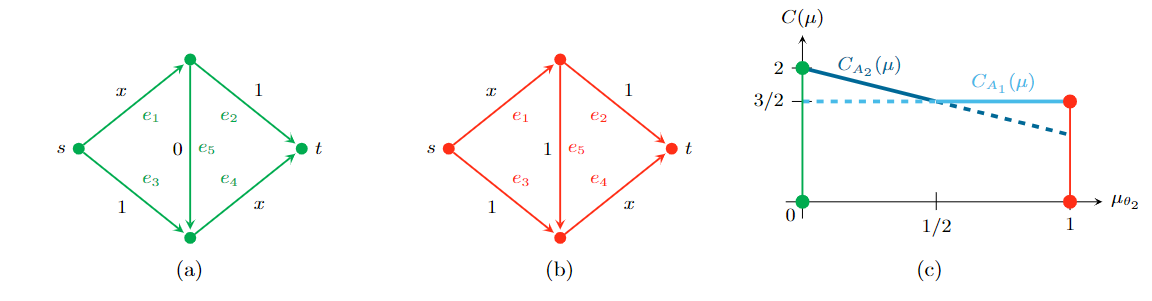
In this example, two different supports appear in the Wardrop equilibria for different beliefs. The support A1 consists of all edges except the middle edge, and the support A2 contains all edges. For support A1, we obtain the Wardrop equilibrium where the flow is equally split among the upper and the lower path. For support A2 we obtain the Wardrop equilibrium where a flow of size 1 – μ2 goes via both the upper and lower path while a flow of size 1 – 2μ2 is routed via the zig-zag-path. This yields the following cost for the supports:
- C(A1(μ)) = 2 · (1/2) · (1/2) + 2 · (1/2) = 3/2
- C(A2(μ)) = 2 · (1 – μ2)(1 – μ2) + 2 · μ2 + (1 – 2 · μ2)μ2 = 2 – μ2
However, for any μ2 < 1/2, the flow defined by support A is not a Wardrop equilibrium for the whole graph, since deviating to the zig-zag-path would reduce private costs. Furthermore, for any μ2 > 1/2, the flow defined by support A2 is not a Wardrop equilibrium for the whole graph since the flow on the middle edge was negative.
Hence, the pointwise minimum is not a concave function, as illustrated in Figure 3. For a prior of μ* = (1/2, 1/2), full information revelation would yield a cost of (1/2) · 2 + (1/2) · 3/2 = 7/4. In contrast, sending a single signal in all states does not reveal any information about the state, so the Wardop equilibrium with a cost of 3/2 emerges. We conclude that full information revelation is not optimal.
In Griesbach et al. [2] we study a similar model with affine costs. In contrast to the model studied in Griesbach et al. [1], the cost functions are deterministic, but the demand in the network is unknown. That is, for each state θ ∈ Θ, there is a demand dθ > 0 that is present in the network. Also for this model, we showed that fully revealing information about the realized demand in the network is always an optimal signaling strategy if and only if the underlying network is series-parallel. We further show that for general networks, an optimal signaling scheme can be computed if a full list of supports that appear in the Wardrop equilibria for some beliefs can be given.
In Griesbach et al. [3], we further studied information design in a dynamic flow model. We consider two nodes V = {s, t} connected by a set of edges E. Every edge e ∈ E has a capacity νe > 0 and a state-dependent travel time be,θ. There is an inflow of flow particles at s with rate 1. Upon arrival, each flow particle chooses an edge to minimize the arrival time at node t. When the inflow rate on an edge exceeds the edge’s capacity, a queue builds up. The time a flow particle spends on an edge equals the waiting time in the queue plus the travel time on the edge. As before, we assume that the flow particles do not know the exact travel times, but have a prior belief about the state. The system operator who knows the state is interested in revealing information about the state to maximize the throughput in the system up to a given time horizon. We give a multiplicative polynomial-time approximation scheme (FPTAS) that, for given ε > 0, computes in polynomial time a (1 – ε)-approximation to the optimal throughput that can be achieved by a public signaling scheme. The PTAS is based on the observation that the throughput is a piecewise quadratic function of the prior. We then use a cell decomposition approach to compute a piecewise affine (1 – ε)-underestimator of the throughput function that ultimately yields the FPTAS.
We also give an additive polynomial-time approximation scheme (PTAS) that approximates the throughput achievable by public signaling schemes up to an arbitrary small additive error ε > 0. This approximation scheme is based on a dual formulation of the optimal signaling problem. The dual problem has infinitely many constraints but can be solved approximately with the Ellipsoid method since we show that the separation problem can be solved in polynomial time by a cell decomposition technique.
Information Exploitation
We also study how information can be exploited in a networked environment. Specifically, we are given an undirected graph G = (V, E) with a designated root vertex r ∈ V. Each edge has a cost ce ≥ 0 measuring the time to establish a connection. There is a treasure hidden at one of the vertices v ≠ r. We assume that an agent is located at time 0 at the root vertex and can establish one of the adjacent edges during a period equal to the corresponding cost. Once a connection is established, the agent can move without cost in the established network. This process models situations where connection lines (e.g. for electricity) have to be created or restored, or where mining operations have to be undertaken. Our goal is to minimize the expected time until the treasure is connected to the root vertex.
In Griebach et al. [4] we show that this problem is hard to approximate by a certain small factor, thus ruling out the existence of an FPTAS or a PTAS. We then devise approximation algorithms for the problem. We give a polynomial 2e-approximation for the case that all vertices have the same probability of containing the treasure and a polynomial (2e + ε)-approximation for every ε > 0 for the case where the vertex may have different probabilities of containing the treasure.
In Disser et al. [5] we further study an incremental variant of the problem.
External Website
Related Publications
[1] Public Signals in Network Congestion Games (Svenja M. Griesbach, Martin Hoefer, Max Klimm, and Tim Koglin)
EC 2022 – Proc. 23rd ACM Conference on Economics and Computation, pp. 736.
[2] Information Design for Congestion Games with Unknown Demand (Svenja M. Griesbach, Martin Hoefer, Max Klimm, and Tim Koglin)
AAAI 2024 – Proc. 38th Annual Conference on Artificial Intelligence, pp. 9722–9730.
[3] Optimizing Throughput and Makespan of Queuing Systems by Information Design (Svenja M. Griesbach, Max Klimm, Philipp Warode, and Theresa Ziemke)
ESA 2024 – Proc. 32nd European Symposium on Algorithms, to appear.
[4] Improved Approximation Algorithms for the Expanding Search Problem (Svenja M. Griesbach, Felix Hommelsheim, Max Klimm, and Kevin Schewior)
ESA 2023 – Proc. 31st European Symposium on Algorithms, pp. 54:1–54:15.
[5] Bicriterial Approximation for the Incremental Prize-Collecting Steiner-Tree Problem (Yann Disser, Svenja M. Griesbach, Max Klimm, and Annette Lutz)
ESA 2024 – Proc. 32nd European Symposium on Algorithms, to appear.
Short introduction to the project
(in german)

