Project
AA2-16
Tailored Entangled Photon Sources for Quantum Technology
Project Heads
Sven Burger, Stephan Reitzenstein
Project Members
Felix Binkowski
Project Duration
01.04.2022 − 31.03.2025
Located at
ZIB
Description
The project aims at developing and employing numerical methods for simulation and optimization of coupled emitter – cavity systems, and to use these methods for designing systems of quantum dots coupled to integrated, high-Q microcavities for state engineering. Further, we aim at coupling efficiency enhancement for integrated, waveguide-coupled setups. A main goal is the investigation and development of contour-integral-based methods for eigensolvers and for resonance expansion, and their application to topical devices for photonic quantum technology. A schematics of a contour-integral-based resonance expansion is depicted in Fig. 1.
Research results of this project include the numerical optimization of fiber-coupled single-photon sources [1] and of photonic crystal cavities [2], a new method to compute eigenfrequency sensitivities [3], a method for resonance expansions of quadratic quantities [4], a method for the computation of poles and zeros and their sensitivities [5], the accurate and efficient numerical computation of eigenfrequency sensitivities near exceptional points [6] (see Fig. 2), and approaches for the rational approximation of photonic response functions with the AAA algorithm [7-10] (see Figs. 3-5). Further research results of this project include applications of the developed methods to systems of emitters and plasmonic and nanooptical resonators [11-19] and to state engineering of quantum gases [20].
Research data and software have been made available via open access data publications [21-31], and further related works have been published [32-36].
External Website
Related Publications
- Numerical optimization of single-mode fiber-coupled single-photon sources based on semiconductor quantum dots, Lucas Bremer, Carlos Jimenez, Simon Thiele, Ksenia Weber, Tobias Huber, Sven Rodt, Alois Herkommer, Sven Burger, Sven Höfling, Harald Giessen, Stephan Reitzenstein. Opt. Express 30, 15913 (2022)
- Fabrication uncertainty guided design optimization of a photonic crystal cavity by using Gaussian processes, Matthias Plock, Felix Binkowski, Lin Zschiedrich, Philipp-Immanuel Schneider, Sven Burger, J. Opt. Soc. Am. B 41, 850 (2024)
- Computation of eigenfrequency sensitivities using Riesz projections for efficient optimization of nanophotonic resonators, Felix Binkowski, Fridtjof Betz, Martin Hammerschmidt, Philipp-Immanuel Schneider, Lin Zschiedrich, Sven Burger, Commun. Phys. 5, 202 (2022)
- Resonance expansion of quadratic quantities with regularized quasinormal modes, Fridtjof Betz, Felix Binkowski, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Phys. Status Solidi A 220, 2200892 (2023)
- Poles and zeros in non-Hermitian systems: Application to photonics, Felix Binkowski, Fridtjof Betz, Remi Colom, Patrice Genevet, Sven Burger, Phys. Rev. B 109, 045414 (2024)
- Computing eigenfrequency sensitivities near exceptional points, Felix Binkowski, Julius Kullig, Fridtjof Betz, Lin Zschiedrich, Andrea Walther, Jan Wiersig, Sven Burger, Physical Review Research 6, 023148 (2024)
- Efficient rational approximation of optical response functions with the AAA algorithm, Fridtjof Betz, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Felix Binkowski, Laser Photonics Rev. 18, 2400584 (2024)
- A Framework to Compute Resonances Arising from Multiple Scattering, Jan David Fischbach, Fridtjof Betz, Nigar Asadova, Pietro Tassan, Darius Urbonas, Thilo Stöferle, Rainer F. Mahrt, Sven Burger, Carsten Rockstuhl, Felix Binkowski, Thomas Jebb Sturges, Adv. Theory Simul. 8, 2400989 (2025)
- Resonance modes in microstructured photonic waveguides: Efficient and accurate computation based on AAA rational approximation, Felix Binkowski, Fridtjof Betz, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Nanophotonics 14, 1665 (2025)
- Uncovering hidden resonances in non-hermitian systems with scattering thresholds, Fridtjof Betz, Felix Binkowski, Jan David Fischbach, Nick Feldman, Lin Zschiedrich, Carsten Rockstuhl, A. Femius Koenderink, Sven Burger, Laser Photonics Rev. 19, e00811 (2025)
- Crossing of the branch cut: the topological origin of a universal 2π-phase retardation in non-Hermitian metasurface, Remi Colom, Elena Mikheeva, Karim Achouri, Jesus Zuniga-Perez, Nicolas Bonod, Olivier J. F. Martin, Sven Burger, Patrice Genevet, Laser Photonics Rev. 17, 2200976 (2023)
- Enhanced Purcell factor for nanoantennas supporting interfering resonances, Remi Colom, Felix Binkowski, Fridtjof Betz, Yuri Kivshar, Sven Burger, Phys. Rev. Research 4, 023189 (2022)
- Onset of Chirality in Plasmonic Meta-molecules and Dielectric Coupling, Kevin Martens, Timon Funck, Eva Y. Santiago, Alexander O. Govorov, Sven Burger, Tim Liedl, ACS Nano 16, 16143 (2022)
- Chiral bio-inspired plasmonics: a paradigm shift for optical activity and photochemistry, Oscar Avalos-Ovando, Eva Yazmin Santiago, Artur Movsesyan, Xiang-Tian Kong, Peng Yu, Lucas V. Besteiro, Larousse Khosravi Khorashad, Hiromi Okamoto, Joseph M. Slocik, Miguel Correa-Duarte, Miguel Comesana-Hermo, Tim Liedl, Gil Markovich, Sven Burger, Alexander O. Govorov, ACS Photonics 9, 2219 (2022)
- Plasmonic nanocrystals with complex shapes for photocatalysis and growth: Contrasting anisotropic hot-electron generation with the photothermal effect, Artur Movsesyan, Eva Yazmin Santiago, Sven Burger, Miguel A. Correa-Duarte, Lucas V. Besteiro, Zhiming Wang, Alexander O. Govorov, Adv. Opt. Mater. 10, 2102663 (2022)
- Colloidal Titanium Nitride Nanobars for Broadband Inexpensive Plasmonics and Photochemistry from Visible to Mid-IR Wavelengths, Sourav Rej, Eva Yazmin Santiago, Olga Baturina, Yu Zhang, Sven Burger, Stepan Kment, Alexander O. Govorov, Alberto Naldoni, Nano Energy 104, 107989 (2022)
- Asymmetric phase modulation with light with parity-symmetry broken metasurfaces, Elena Mikheeva, Remi Colom, Karim Achouri, Adam Overvig, Felix Binkowski, Jean-Yves Duboz, Sebastien Cueff, Shanhui Fan, Sven Burger, Andrea Alú, Patrice Genevet, Optica 10, 1287 (2023)
- Chiral and directional optical emission from a dipole source coupled to a helical plasmonic antenna, Lilli Kuen, Lorenz Löffler, Aleksei Tsarapkin, Lin Zschiedrich, Thorsten Feichtner, Sven Burger, Katja Höflich, Appl. Phys. Lett. 124, 231102 (2024)
- A tiny Drude scatterer can accurately model a coherent emitter in nanophotonics, Felix Binkowski, Sven Burger, Günter Kewes, Nanophotonics 13, 4537 (2024)
- Bayesian optimization for state engineering of quantum gases, Gabriel Müller, VJ Martínez-Lahuerta, Ivan Sekulic, Sven Burger, Philipp-Immanuel Schneider, Naceur Gaaloul, preprint arXiv:2404.18234 (2024)
- RPExpand, Fridtjof Betz, Felix Binkowski, Sven Burger, Zenodo, DOI: 10.5281/zenodo.7840116 (2023)
- Source code and simulation results for nanoantennas supporting an enhanced Purcell factor due to interfering resonances, Remi Colom, Felix Binkowski, Fridtjof Betz, Yuri Kivshar, Sven Burger, Zenodo, DOI:10.5281/zenodo.6565850 (2022)
- Source code and simulation data for Computation of eigenfrequency sensitivities using Riesz projections for efficient optimization of nanophotonic resonators, Felix Binkowski, Fridtjof Betz, Martin Hammerschmidt, Philipp-Immanuel Schneider, Lin Zschiedrich, Sven Burger, Zenodo, DOI:10.5281/zenodo.6614951 (2022)
- Source code and simulation results for computing resonance expansions of quadratic quantities with regularized quasinormal modes, Fridtjof Betz, Felix Binkowski, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Zenodo, DOI: 10.5281/zenodo.7376556 (2022)
- Source code and simulation results: Poles and zeros of electromagnetic quantities in photonic systems, Felix Binkowski, Fridtjof Betz, Rèmi Colom, Patrice Genevet, Sven Burger, Zenodo, DOI: 10.5281/zenodo.8063931 (2023)
- Research data for “Fabrication uncertainty guided design optimization of a photonic crystal cavity by using Gaussian processes”, Matthias Plock, Felix Binkowski, Lin Zschiedrich, Philipp-Immanuel Schneider, Sven Burger, Zenodo, DOI: 10.5281/zenodo.8131611 (2024)
- Source code and simulation results: Computing eigenfrequency sensitivities near exceptional points, Felix Binkowski, Julius Kullig, Fridtjof Betz, Lin Zschiedrich, Andrea Walther, Jan Wiersig, Sven Burger, Zenodo, DOI: 10.5281/zenodo.10715639 (2024)
- Source Code and Simulation Results: Chiral and directional optical emission from a dipole source coupled to a helical plasmonic antenna, Lilli Kuen, Lorenz Löffler, Aleksei Tsarapkin, Lin Zschiedrich, Thorsten Feichtner, Sven Burger, Katja Höflich, Zenodo, DOI: 10.5281/zenodo.10598255 (2024)
- Source code and simulation results: Efficient rational approximation of optical response functions with the AAA algorithm, Fridtjof Betz, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Felix Binkowski, Zenodo, DOI: 10.5281/zenodo.10853692 (2024)
- Source code and simulation results: Resonance modes in microstructured photonic waveguides – Efficient and accurate computation based on AAA rational approximation, Felix Binkowski, Fridtjof Betz, Martin Hammerschmidt, Lin Zschiedrich, Sven Burger, Zenodo, DOI: 10.5281/zenodo.14202408 (2025)
- Source code and simulation results: Uncovering hidden resonances in non-hermitian systems with scattering thresholds, Fridtjof Betz, Felix Binkowski, Jan David Fischbach, Nick Feldman, Lin Zschiedrich, Carsten Rockstuhl, A. Femius Koenderink, Sven Burger, Zenodo, DOI: 10.5281/zenodo.15880360 (2025)
- T-matrix representation of optical scattering response: Suggestion for a data format, N. Asadova, K. Achouri, K. Arjas, B. Ajuguie, R. Aydin, A. Baron, D. Beutel, B. Bodermann, K. Boussaoud, S. Burger, M. Choi, K. Czajkowski, A. B. Evlyukhin, A. Fazel-Najafabadi, I. Fernandez-Corbaton, P. Garg, D. Globosits, U. Hohenester, H. Kim, S. Kim, P. Lalanne, E. C. L. Ru, J. Meyer, J. Mun, L. Patelli, L. Pflug, C. Rockstuhl, J. Rho, S. Rotter, B. Stout, P. Torma, J. O. Trigo, F. Tristram, N. L. Tsitsas, R. Vallee, K. Vynck, T. Weiss, P. Wiecha, T. Wriedt, V. Yannopapas, M. A. Yurkin, G. P. Zouros, J. Quant. Spectrosc. Radiat. Transf. 333, 109310 (2025)
- Optics for terawatt-scale photovoltaics: review and perspectives, K. Jäger, U. Aeberhard, E. A. Llado, B. Bläsi, S. Burger, B. Ehrler, W. Favre, A. Fejfar, T. Gageot, I. Gordon, H. Helmers, O. Höhn, O. Isabella, M. Jost, M. Ledinsky, J. Mandal, P. Manley, D. Munoz, Z. Omair, J. C. O. Lizcano, U. W. Paetzold, A. P. Raman, H. Sai, R. Saive, M. Schmid, E. Yablonovitch, C. Becker, Adv. Opt. Photonics 17, 185 (2025)
- Spectroscopic ellipsometry of plasmonic gratings – ideal parameters for sensing and subpicometer measurement uncertainty, D. Mukherjee, S. Burger, T. Siefke, J. Gour, B. Bodermann, P. Petrik, ACS Omega 10, 14466 (2025)
- Optimizing aesthetic appearance of perovskite solar cells using color filters, J. Schaible, H. Winarto, V. Skorjanc, D. Yoo, L. Zimmermann, K. Jäger, I. Sekulic, P.-I. Schneider, S. Burger, A. Wessels, B. Bläsi, C. Becker, Solar RRL 9, 2400627 (2025)
- Chiral plasmonic crystals selfassembled by dna origami, C. Sikeler, S. Kempter, I. Sekulic, S. Burger, T. Liedl, J. Phys. Chem. C 129, 5116 (2025)
Related Pictures

Fig. 1. Schematics: Contour integrations in the complex frequency plane. The contours (dashed lines) encircling resonance frequencies (red crosses) allow to determine the corresponding modal fields. The outer contour (solid line) allows for evaluating the background contribution to the modal expansion of the field caused by the emitter at a real frequency.

Fig. 2. Combining contour integration and algorithmic differentiation yields eigenfrequency sensitivities near exceptional points. The sketch shows the electric field intensity near an exceptional point in a microdisk cavity.

Fig. 3. Rational approximation of the optical response of a metasurface. The approximation is based on sample points in the complex frequency plane and gives the poles, zeros, and residues of the underlying meromorphic function. The AAA algorithm can be used to compute the approximation.
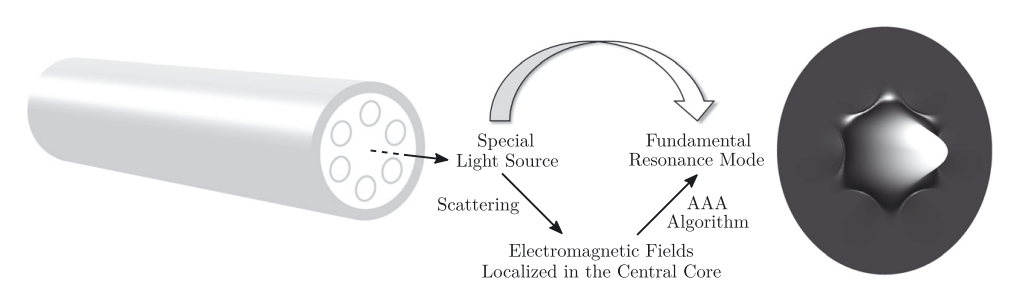
Fig. 4. Computation of the fundamental resonance mode of a microstructured waveguide. The waveguide is illuminated with a light source located at the center of the system. The resulting scattered electromagnetic fields are superposed based on AAA rational approximation. The light source is chosen so that it couples mainly with the fundamental resonance mode and not with other modes. This special choice of the source enables an efficient and accurate computation of the fundamental resonance mode of the system.

Fig. 5. The points where diffraction orders emerge or vanish in the propagating spectrum of periodic non-Hermitian systems are referred to as scattering thresholds. Close to these branch points, resonances from different Riemann sheets can tremendously impact the optical response. However, these resonances are so far elusive for two reasons. First, their contribution to the signal is partially obscured, and second, they are inaccessible for standard computational methods. Here, the interplay of scattering thresholds with resonances is explored and a multi-valued rational approximation is introduced to access the hidden resonances.

