Project
AA1-6
Data-Driven Modeling from Atoms to Cells
Project Heads
Frank Noé, Cecilia Clementi (since January 2021), Christof Schütte
Project Members
Péter Bernát Szabó (since 01/2024), Maaike Galama (11/2022 – 09/2023), Paolo Andrea Erdman (12/2020 – 12/2022), Simon Olsson (01/2019 – 09/2020)
Project Duration
First funding period: 01.01.2019 – 31.12.2020; Second funding period: 01.01.21 – 31.12.2022; Third funding period: 01.11.2022 – 31.10.2025
Located at
FU Berlin
Description
Living and reconstituted biological systems involve a large range of time- and lengthscales. These scales are coupled, e.g., a single-point mutation that changes only a few atoms in a protein can disrupt the biochemical processes this protein is involved in and eventually cause fatal damage to the organism, e.g., in cancer and other diseases. To make matters even more difficult, most subcellular processes operate below the diffraction limit: Light that does not damage biological matter cannot resolve structures smaller than 250 nanometers – thus any process involving molecules or other small cellular structures cannot be directly visualized.
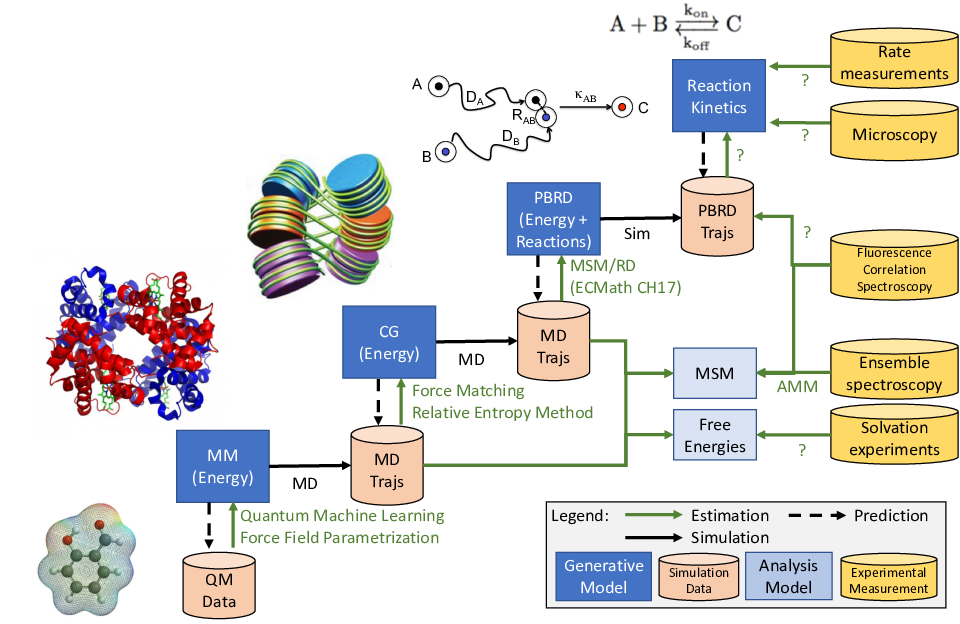
As a result, no single simulation model or experiment can provide a complete analysis of biological systems that reveals all scales. Hence, there is a large zoo of (often ad hoc) simulation and measurement techniques that each probe different scales and make different approximations or accept different kinds of biases or uncertainties (Fig. 1). The small lengthscales below the diffraction limit have the additional complication that the variables of computer simulations cannot be directly validated by observation, as experiments on these scales can only access expectation values or time-series of low-dimensional experimental observables.
The MATH+ proposal cites two main challenges for AA1 that exist on each of these scales: the timescale barrier and the accuracy barrier. The timescale barrier means that, at each of the high-resolution scales, a direct simulation of the complete system (e.g. cell or organism) over functionally relevant timescales is computationally unfeasible. In this project we focus on the accuracy barrier. Citing from the MATH+ proposal:
The accuracy barrier is related to the fact that every model of life processes is inherently parametric. Especially models that operate at higher levels of resolution, (…) such as in cellular processes, cannot guarantee an accurate description with a general and transferable parameter set, as there are missing degrees of freedom. To address this problem, hybrid models that couple different resolutions are required, and systematic data integration techniques that are able to incorporate measurements at all levels of resolution are critical.
This central problem of AA1 is directly addressed in the present project. More concretely, we ask: How can we optimally estimate the model parameters of simulation models by combining simulation and measurement data at different scales? This question is, as yet, not addressed in a unified and systematic approach that is reproducible, testable and applicable over many or all scales. Existing approaches from other areas are only partially transferable because of the stochastic nature and observability limits of life science processes.
Project Webpages
Selected Publications
- Patrick Bryant et al. “Structure Prediction of Protein-Ligand Complexes from Sequence Information with Umol”. In: Nature Communications 15.1 (May 28, 2024), p. 4536.
- P. Bernat Szabo et al. An Improved Penalty-Based Excited-State Variational Monte Carlo Approach with Deep-Learning Ansatzes. May 27, 2024. doi: 10.48550/arXiv.2405.17089.
- Paolo Abiuso et al. “Optimal thermometers with spin networks”. In: Quantum Science and Technology (2024).
- Gian Marcello Andolina et al. Dicke Superradiant Enhancement of the Heat Current in Circuit QED. Jan. 30, 2024. arXiv: 2401.1746
- Hao Wu and Frank No ́e. “Reaction Coordinate Flows for Model Reduction of Molecular Kinetics”. In: The Journal of Chemical Physics 160.4 (Jan. 25, 2024), p. 044109.
- Nicholas E. Charron et al. Navigating Protein Landscapes with a Machine-Learned Transferable Coarse-Grained Model. Oct. 27, 2023. arXiv: 2310.1827
- Maciej Majewski et al. “Machine Learning Coarse-Grained Potentials of Protein Thermodynamics”. In: Nature Communications 14.1 (Sept. 15, 2023), p. 5739.
- Marloes Arts et al. “Two for One: Diffusion Models and Force Fields for Coarse-Grained Molecular Dynamics”. In: Journal of Chemical Theory and Computation 19.18 (Sept. 26, 2023), pp. 6151–6159.
- PA Erdman, F Noé: Model-free optimization of power/efficiency tradeoffs in quantum thermal machines using reinforcement learning. PNAS Nexus, pgad248 (2023)
- L Klein, A Krämer, F Noé: Equivariant flow matching. preprint arXiv:2306.15030 (2023)
- PA Erdman, A Rolandi, P Abiuso, M Perarnau-Llobet, F Noé: Pareto-optimal cycles for power, efficiency and fluctuations of quantum heat engines using reinforcement learning. Phys. Rev. Res. 5, L022017 (2023)
- A Krämer, AE Durumeric, NE Charron, Y Chen, C Clementi, F Noé: Statistically optimal force aggregation for coarse-graining molecular dynamics. J. Phys. Chem. Lett. 14, 17, 3970–3979 (2023)
- MM Galama, H Wu, A Krämer, M Sadeghi, F Noé: Stochastic Approximation to MBAR and TRAM: Batchwise Free Energy Estimation. J. Chem. Theory Comput. 19, 3, 758–766 (2023)
- J Köhler, Y Chen, A Krämer, C Clementi, F Noé: Flow-matching: Efficient coarse-graining of molecular dynamics without forces. J. Chem. Theory Comput. 19, 3, 942-952 (2023)
- MT Entwistle, Z Schätzle, PA Erdman, J Hermann, F Noé: Electronic excited states in deep variational Monte Carlo. Nat. Commun. 14, 274 (2023)
- P Bryant, F Noe: Improved protein complex prediction with AlphaFold-multimer by denoising the MSA profile. bioRxiv, 2023-07 (2023)
- PA Erdman, GM Andolina, V Giovannetti, F Noé: Reinforcement learning optimization of the charging of a Dicke quantum battery. arXiv preprint arXiv:2212.12397 (2022)
- T Le, F Noé, DA Clevert: Representation Learning on Biomolecular Structures using Equivariant Graph Attention. In Learning on Graphs Conference (pp. 30-1). PMLR (2022)
- A Mardt, T Hempel, C Clementi, F Noé: Deep learning to decompose macromolecules into independent Markovian domains. Nat. Commun. 13, 7101 (2022)
- F Musil, I Zaporozhets, F Noé, C Clementi, V Kapil: Quantum dynamics using path integral coarse-graining. J. Chem. Phys. 157, 181102 (2022)
- P Abiuso, PA Erdman, M Ronen, F Noé, G Haack, M Perarnau-Llobet: Discovery of Optimal Thermometers with Spin Networks aided by Machine-Learning. arXiv preprint arXiv:2211.01934 (2022)
- M Dibak, L Klein, A Krämer, F Noé: Temperature steerable flows and Boltzmann generators. Phys. Rev. Research 4, L042005 (2022)
- J Hermann, J Spencer, K Choo, A Mezzacapo, WMC Foulkes, D Pfau, G Carleo, F Noé: Ab-initio quantum chemistry with neural-network wavefunctions. Nat Rev Chem (2023)
- KS Chakrabarti, S Olsson, S Pratihar, K Giller, K Overkamp, KO Lee, V Gapsys, K Ryu, BL de Groot, F Noé, S Becker, D Lee, TR Weikl, C Griesinger: A litmus test for classifying recognition mechanisms of transiently binding proteins. Nat. Commun. 13, 3792 (2022)
- PA Erdman, F Noé: Driving black-box quantum thermal machines with optimal power/efficiency trade-offs using reinforcement learning. arXiv preprint arXiv:2204.04785 (2022)
- PA Erdman, F Noé: Identifying optimal cycles in quantum thermal machines with reinforcement-learning. npj Quantum Information, 8, 1 (2022)
- M Hoffmann, M Scherer, T Hempel, A Mardt, B de Silva, BE Husic, S Klus, H Wu, N Kutz, SL Brunton, F Noé: Deeptime: a Python library for machine learning dynamical models from time series data. Mach. Learn.: Sci. Technol. 3 015009 (2021)
- A Mardt, F Noé: Progress in deep Markov state modeling: Coarse graining and experimental data restraints. J. Chem. Phys. 155, 214106 (2021)
- J Köhler, A Krämer, F Noé: Smooth normalizing flows. NeurIPS, 34, 2796-2809 (2021)
- R Winter, F Noé, DA Clevert: Permutation-invariant variational autoencoder for graph-level representation learning. NeurIPS, 34, 9559-9573 (2021)
- MJ Del Razo, M Dibak, C Schütte, F Noé: Multiscale molecular kinetics by coupling Markov state models and reaction-diffusion dynamics. J. Chem. Phys. 155, 124109 (2021)
- Y Chen, A Krämer, NE Charron, BE Husic, C Clementi, F Noé: Machine learning implicit solvation for molecular dynamics. J. Chem. Phys. 155, 084101 (2021)
- T Hempel, MJ Del Razo, CT Lee, BC Taylor, RE Amaro, F Noé: Independent Markov decomposition: Toward modeling kinetics of biomolecular complexes. Proc. Natl. Acad. Sci. U.S.A. 118(31):e2105230118 (2021)
- J Wang, NE Charron, BE Husic, S Olsson, F Noé, C Clementi: Multi-body effects in a coarse-grained protein force field. J. Chem. Phys. 154, 164113 (2021)
- L Sbailò, M Dibak, F Noé: Neural mode jump monte carlo. J. Chem. Phys. 154, 074101 (2021)
- L Raich, K Meier, J Günther, CD Christ, F Noe, S Olsson: Discovery of a hidden transient state in all bromodomain families. BioRxiv Doi:10.1101/2020.04.01.019547 (2020)
- F Noé, A Tkatchenko, KR Müller, C Clementi: Machine learning for molecular simulation. Annu. Rev. Phys. Chem. 71, 361-390 (2020)
- F Noé, G De Fabritiis, C Clementi: Machine learning for protein folding and dynamics, Curr. Opin. Struct. Biol. 60, 77-84 (2020)
- R Winter, J Retel, F Noé, DA Clevert, A Steffen: grünifai: Interactive multi-parameter optimization of molecules in a continuous vector space. Bioinformatics (2020)
- J Wang, S Olsson, C Wehmeyer, A Pérez, NE Charron, G De Fabritiis, F. Noé, C. Clementi: Machine learning of coarse-grained molecular dynamics force fields. ACS Central Sci. 5, 755-767 (2019)
- J Hermann, Z Schätzle, F Noé: Deep neural network solution of the electronic Schrödinger equation. Preprint arXiv:1909.08423 (2019)
- M Hoffmann, F Noé: Generating valid Euclidean distance matrices. Preprint arXiv:1910.03131 (2019)
- S Klus, BE Husic, M Mollenhauer, F Noé: Kernel methods for detecting coherent structures in dynamical data. Chaos 29, 123112 (2019)
- J Köhler, L Klein, F Noé: Equivariant Flows: sampling configurations for multi-body systems with symmetric energies. Preprint arXiv:1910.00753 (2019)
- F Noé, S Olsson, J Köhler, H Wu: Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning. Science 365, eaaw1147 (2019)
- J Wang, S Chmiela, KR Müller, F Noè, C Clementi: Ensemble Learning of Coarse-Grained Molecular Dynamics Force Fields with a Kernel Approach. J. Chem. Phys. (in press, preprint arXiv:2005.01851)
- R Winter, F Montanari, F Noé, DA Clevert: Learning continuous and data-driven molecular descriptors by translating equivalent chemical representations. Chem. Sci. 10, 1692-1701 (2019)
- R Winter, F Montanari, A Steffen, H Briem, F Noé, DA Clevert: Efficient multi-objective molecular optimization in a continuous latent space. Chem. Sci. 10 (34), 8016-8024 (2019)
- M Dibak, C Fröhner, F Noé, F Höfling. Diffusion-influenced reaction rates in the presence of pair interactions. J. Chem. Phys. 151, 164105 (2019)
- F Paul, H Wu, M Vossel, BL de Groot, F Noé: Identification of kinetic order parameters for non-equilibrium dynamics. J. Chem. Phys. 150, 164120 (2019)
Selected Pictures
Please insert any kind of pictures (photos, diagramms, simulations, graphics) related to the project in the above right field (Image with Text), by choosing the green plus image on top of the text editor. (You will be directed to the media library where you can add new files.)
(We need pictures for a lot of purposes in different contexts, like posters, scientific reports, flyers, website,…
Please upload pictures that might be just nice to look at, illustrate, explain or summarize your work.)
As Title in the above form please add a copyright.
And please give a short description of the picture and the context in the above textbox.
Don’t forget to press the “Save changes” button at the bottom of the box.
If you want to add more pictures, please use the “clone”-button at the right top of the above grey box.

