“Tagesspiegel” Article on Interdisciplinary MATH+ Research Project @TU Berlin, Max Klimm Interview, and Film on “Game Theory”

The Berlin newspaper “Tagesspiegel“ has recently published an article on the interdisciplinary MATH+ research project, “Evolution Models for Historical Networks,” by Max Klimm and his colleagues. On this occasion, MATH+ interviewed him on a few more MATH+ projects and released his short film on “Game Theory,” produced by the Berlin University Alliance (BUA).
Max Klimm has been a tenure-track professor for “Discrete Optimization” at Technische Universität Berlin (TU Berlin) since July 2020. His current research interests are in algorithmic game theory, discrete optimization, efficient algorithms, operations research, and mechanism design. He received his PhD in mathematics from TU Berlin in 2012 as a member of the Berlin Mathematical School (BMS). He held a postdoctoral position from 2012 to 2014 and led the ECMath junior research group “Optimization under Uncertainty” from 2014 to 2016, both positions at TU Berlin. Subsequently, Max Klimm accepted the call for a tenure-track assistant professorship in “Operations Research” at the Faculty of Economics of Humboldt-Universität zu Berlin and became Principal Investigator (PI) at MATH+ in 2019.
INTERVIEW:
Dear Max, how did you actually develop an interest in mathematics, and why did you choose to study mathematics?
I was interested in many things during my school years, but I always liked the fact that there was such a thing as right or wrong in math. Compared to school lessons, where we mainly did a lot of calculations, studying math at university is more about proof and understanding connections.
So, how did you become interested in your research topics?
Especially in “Discrete Optimization,” I found the application aspect very exciting. Classical discrete optimization problems, such as calculating the network’s shortest path, are often simple to describe but challenging to solve. One application of this problem, for example, is in navigation systems. I was fascinated by these problems, also because they were not taught at school. That’s why I delved into this topic and then stuck with it.
Can you briefly describe the topic of your research group, “Discrete Optimization,” at the Technische Universität Berlin?
We look at optimization problems on discrete structures like networks or more abstract entities like matroids. The difference between discrete and continuous mathematics can be understood by the shortest path example. With continuous methods, the complete movement of a particle in space over time could be described. With navigation systems, however, one is only interested in which roads are being used rather than necessarily in the centimeter-precise location of the vehicle on the road. If we only consider the roads used, we get a discrete problem since a city has only a finite number of roads. This is an abstraction that allows us to solve even more significant issues.
Can this network research also be applied to social networks?
That’s the beauty of mathematics because the mathematical notion of a graph is general enough to represent various pairwise relationships. These can be roads, telecommunication, social, or even historical networks that can be described using the same mathematics. A graph usually has a finite set of nodes; these can be intersections in the road graph or people in social networks. An edge between two nodes represents a reciprocal or unilateral relationship between these points. In the case of the road graph, this means that I can move from one point to another on the road, and in the case of the social network, the two nodes can be friends.
You deal a lot with “Game Theory,” and we just published your short film on Game Theory. What is so fascinating about it?
During my studies abroad in Paris at the École Polytechnique, I came into contact with game theory for the first time. Since then, I have found it an incredibly fascinating field because you can explain many dynamics of human interaction by using only numbers. For example, I can use it to describe simple games such as “Rock, Paper, Scissors” by transforming it into a matrix. I then have a table with one row for each player’s strategy and one column for the other, thus three rows and three columns. Then I write in the corresponding table entries what the benefit of each combination is. For example, if player 1 chooses rock and player 2 chooses paper, player 2 wins. If I now look at the table with a total of 18 numbers, I can predict a good strategy, i.e., how it should be played and the likely outcomes. So, it’s fascinating that you can describe and thoroughly analyze the whole game with 18 numbers. The same applies to more complex structures; for example, if an item is sold on eBay, many players must decide how to act and bid to get it. Everyone then has a strategy, and the benefit depends on the strategy of all participants.
One of your MATH+ research projects, “Tropical Mechanism Design,” dealt with auctions and profit maximization. Is that also related to game theory?
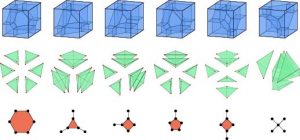
MATH+ project AA3-5 (tropical mech. design)
Exactly. I supervised this project with Michael Joswig, an expert in discrete geometric methods. “Mechanism design” is a buzzword that describes the development of auction formats, and “Tropical” stands for the tropical geometry point of view on these auction formats. The question was whether specific auction formats could be better described with the help of tropical geometry. So far, the mathematical problem of an auctioneer selling one item while maximizing profit has been well understood. Roger Myerson was awarded the “Nobel Memorial Prize in Economic Sciences” for showing that, in this case, a second-price auction with a cleverly chosen starting bid maximizes the profit. The eBay platform offers a starting bid for the item to be sold. The bidding agent then carries out the second-price auction, i.e., all participants enter their respective highest bid, and the highest bidder then pays the amount of the second-highest bid. One can prove mathematically that this auction format with a starting bid maximizes the auctioneer’s profit. However, you may want to sell several goods at the same time. In this case, the mathematical theory still needs to be developed. An example of such a multiple goods auction would be the Spectrum Auctions, for example, when Germany auctioned the UMTS licenses (Universal Mobile Telecommunications System). Here, multiple goods were sold in one auction, namely multiple licenses for different geographic regions and frequency bands. Our research project aimed to better understand this auction situation using geometric methods, and we were able to make progress in this area together with our joint PhD student Sylvain Spitz.
Which research projects and topics are you still working on at MATH+?
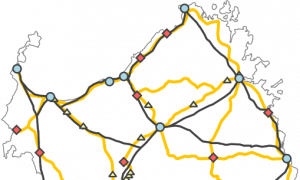
MATH+ Project EF5-6 (historical networks)
The joint project “Evolution Models for Historical Networks” with Guillaume Sagnol and Benjamin Ducke, which will run until 2024, is about reconstructing historical road networks. Here, we specifically looked at the ancient Roman road network of Sardinia. There are certain archaeological findings of what the road network might have looked like at that time, but they are inconclusive. Therefore, with our joint PhD student Maximilian Stahlberg, we have developed a mathematical model that explains how the road network might have evolved over time and compared it to other models. We found that our model can predict the evolution of the road network quite well.
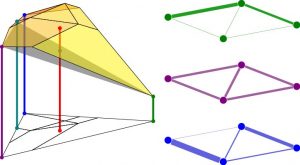
MATH+ Project AA3-9 (information design)
Another ongoing project is “Information Design for Bayesian Networks.” Here we are looking at traffic networks with colleagues from Frankfurt and my PhD student Svenja Griesbach. The travel time in a traffic network is stochastic, i.e., unsure because you don’t know how long the trip from TU Berlin to Alexanderplatz would take right now. It also depends, in particular, on how much traffic there is on the roads. However, traffic service providers, like Google, know the traffic situation during the rush hour. In this project, we are researching the extent to which we can minimize the total travel time and total fuel consumption by revealing information about traffic on the network to road users to achieve a good traffic equilibrium, i.e., an equilibrium with a low total travel time.
Interestingly, it may be beneficial not to reveal all of the information. Instead, it may be more beneficial to only partially share the knowledge to better guide the users’ behavior. Here we examine the mathematical problem of computing optimal information structures that induce the best possible equilibrium in these situations.
What is the aim of your research? Should there be possible applications?
First of all, I understand this as basic research, e.g., the “Mechanism Design” problem or even the “Information Design” problem is highly topical mathematical problems that have not yet been completely understood mathematically. There is no characterization yet for the revenue-maximizing auctions for multiple goods, and there is no information yet about what information transport participants should receive to induce a good equilibrium. But if we gain this understanding, the application relevance would be great since it could improve traffic equilibrium or implement multi-commodity auctions.
After all, the beauty of mathematics is that it takes place in a relatively abstract environment; for example, in the information design of traffic networks, you realize that you need a lot of parametrized flow algorithms to calculate the traffic flows even as traffic volumes change. So, we are interested in learning how the traffic volume changes when there is suddenly more flow in the network. Another project in the SFB Transregio 154 (Collaborative Research Center) is about designing or maintaining hydrogen networks. Here, I use these models and methods to explain how the hydrogen spreads in the network when I increase the pressure. My goal is to stay at a relatively abstract level but always keep in mind what the interesting question might be for a potential application.
Our first explanatory film on the MATH+ YouTube channel is titled “Understanding Complex Systems,” and that’s what mathematics is primarily about.
In my research, I am particularly interested in complex systems in which the usage behavior of the participants plays a role, i.e., huge auction platforms, traffic networks, etc.
The plus in MATH+ also refers to collaboration with other disciplines. Your research project,
“Evolution Models for Historical Networks” is interdisciplinary. Who are you working with, and how is the collaboration going?
One of the goals of MATH+ is to see how mathematical methods can help in other scientific fields. Benjamin Ducke from the German Archaeological Institute (DAI) approached us and asked to what extent mathematical research could help to reconstruct road networks because incomplete data is a classic archaeological problem, as collecting data is highly time-consuming. One needs to carry out excavations for this and some things will never be found. Therefore, the crucial question is how best to deal with the sparse data available. In this project, we have developed a mathematical model that describes how road networks might have evolved and have fitted this model with archaeological evidence found in Sardinia, e.g., waypoints, locations of cities, and also geographic features such as the topology of the land. This allows us to make predictions for this ancient Roman road network that are comparable to or even better than the predictions made by experts after long research in the country.
What are the advantages of such a sizeable mathematical research center as MATH+?
It allows you to think outside the box, collaborate and interact with many colleagues from other scientific disciplines. Also, this interdisciplinary project [on the historical road network in Sardinia with the DAI], in particular, would not have been possible without MATH+ because this form of collaboration is very time-consuming, especially at the beginning, when you need a lot of time to understand the questions on the other side and also to develop the concrete mathematical problem. Fortunately, we were able to finance a PhD position through the Cluster of Excellence MATH+ to work seriously on this interdisciplinary project, which in this case has also worked out well. It is thanks to MATH+ that we were able to initiate the collaboration, which otherwise would never have occurred.
The “Tropic Mechanism Design” project was more of an intra-mathematical issue if you consider game theory an area of mathematics. There is, so to speak, a deficit of understanding of game theory and multicommodity auctions. The question is whether an area of mathematics that at first sight seems quite distant, namely tropical geometry, can help to answer these concrete questions better, which the project has now shown. This is also a project that would have been very difficult to do outside of MATH+, and everyone involved in the project learned a lot mathematically. MATH+ offers an extreme range of mathematical topics and possibilities. I enjoy it enormously, and it is a driving force for me.
What has been the highlight of your career so far?
I can’t name one. I don’t even want to single out individual things. The fact that I have the opportunity to work on such completely different projects here in Berlin and at MATH+, i.e., auctions, traffic networks, and historical networks, makes my work so varied and exciting that every working day is a little highlight.
What else in your work is enriching besides research?
In addition to research, teaching is fundamental. That’s an entirely different requirement, but it’s also a lot of fun, even though it is very time-consuming. That also applies to supervising Master’s and PhD students, which is another challenge. After all, the students and PhD students are involved in the projects and not detached from them. Nevertheless, it makes a difference whether you are active or guiding others to do it. Overall, the extreme range of activities up to this interview is inspiring.
Thank you very much for the interesting interview and the many insights into your work and research!
The interview was conducted by Beate Rogler (MATH+) in April 2023.
——–
LINKS:
-
- “Tagesspiegel” Article on Max Klimm‘s MATH+ Research Project “Evolution Models for Historical Networks”, May 2023 (in German)
- Max Klimm’s Short Film Portrait on “Game Theory,” Produced by the Berlin University Alliance (in German)
- Homepage of Max Klimm at the Technischen Universität Berlin (in English)
- The entire text in German (PDF)

