10.12.2024 In News By rogler

MATH+ Member Carlos Améndola and Co-Authors Win Prestigious SIAM Review SIGEST Award for Outstanding Publication

Sketch of minimizing the norm over a group orbit (left) and maximizing the likelihood over a statistical model (right). The two pictures are connected. Images: © Carlos Amendola et al.

Carlos Améndola, a MATH+ member and Assistant Professor at Technische Universität Berlin, along with collaborators Anna Seigal (Harvard University), Kathlén Kohn (KTH Stockholm), and Philipp Reichenbach (TU Berlin), has been awarded the prestigious SIAM Review SIGEST Award by the Society for Industrial and Applied Mathematics (SIAM). Congratulations!

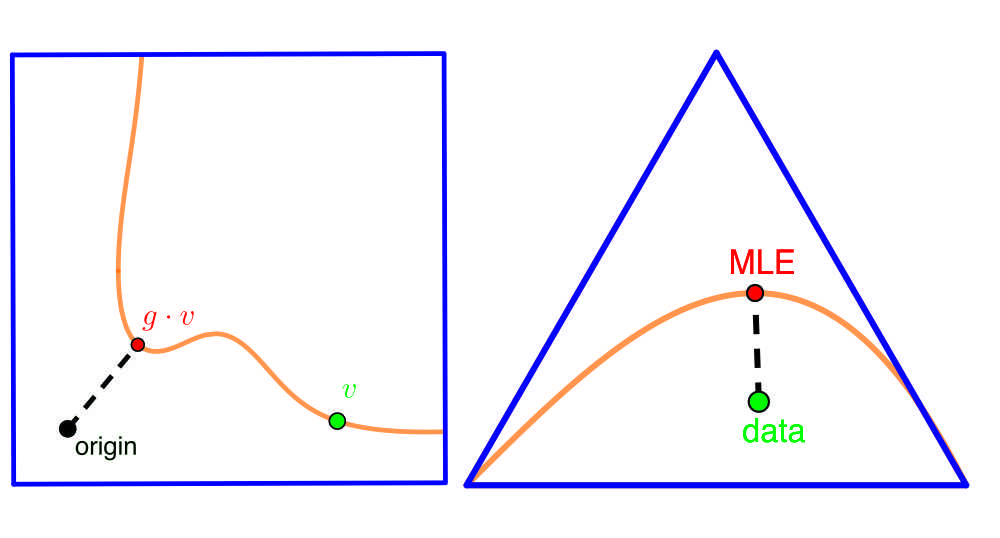
The SIGEST Award recognizes outstanding work that bridges theoretical mathematics and real-world applications, offering innovative tools for addressing complex problems. The team’s paper, “A Bridge between Invariant Theory and Maximum Likelihood Estimation,” earned the award for uncovering profound connections between geometry and statistics—specifically between “geometric invariant theory” and the statistical method “maximum likelihood estimation” (MLE). Notably, three of the four team members completed their PhDs as students of the Berlin Mathematical School (BMS).

Bridging Two Mathematical Worlds

The authors present novel ideas that merge distinct areas of mathematics, offering practical methods that benefit both geometry and statistics. Their work demonstrates how a geometric concept related to stability enhances the understanding of MLE, showing when data-fitting problems for certain mathematical models—such as Gaussian or log-linear models—yields unique and stable solutions. By bridging these fields, the team has introduced innovative methods for addressing challenges in both domains.

Their research also highlights how stability under group actions explains when MLE produces reliable solutions, especially in high-dimensional settings such as Gaussian graphical models and matrix normal models. The team demonstrated that scaling algorithms, traditionally used in statistics, can solve problems in invariant theory and vice versa—opening potential new applications in data science and machine learning. For more details on the award-winning paper, see the SIAM Review publication: https://doi.org/10.1137/20M132893.

Origins of the Research

The seeds for this collaboration were planted in 2017 when Carlos Améndola and Kathlén Kohn were students at the Berlin Mathematical School (BMS). In 2018, Anna Seigal, then a PhD student at UC Berkeley, joined  their research group, even traveling to Germany to facilitate the collaboration. The foundation of this award-winning research was laid in 2019 when the trio participated in the MATH+ Thematic Einstein Semester (TES) on “Algebraic Geometry – Varieties, Polyhedra, Computation.” The team was fully formed later that year when Philipp Reichenbach joined them after the Thematic Einstein Semester. At the time, Reichenbach was also a BMS PhD student at TU Berlin, funded by an ERC grant from Peter Bürgisser (TU Berlin). His PhD thesis “Invariant Theory in Computational Complexity and Algebraic Statistics,” extensively references the group’s work. The collaboration flourished under the mentorship and support of Bernd Sturmfels, director at the Max-Planck Institute for Mathematics in the Sciences in Leipzig. Sturmfels encouraged the group to delve deeper into this research topic. Their discussions uncovered a profound intersection between geometric invariant theory and maximum likelihood estimation (MLE), a cornerstone of statistical modeling.

 

Reflecting on the recognition, Carlos Améndola shared: “I am deeply honored to receive the SIGEST Award together with my co-authors. This project was the result of years of collaboration, including an inspiring visit to UC Berkeley to meet my colleagues and remote teamwork during the pandemic. This recognition motivates us to further explore the rich connections between algebra, geometry and statistics.“

About Carlos Améndola

Carlos Enrique Améndola Cerón is a mathematician and Assistant Professor at TU Berlin. His research focuses on algebraic statistics, an area that integrates commutative algebra, algebraic geometry, probability, and statistics.

Améndola earned his PhD in Mathematics from TU Berlin in 2017 as part of the Berlin Mathematical School (BMS). He has held postdoctoral positions at TU Munich and the Max-Planck Institute for Mathematics in the Sciences in Leipzig (MiS). Subsequently, he served as a “substitute professor” (Vertretungsprofessor) at the Institute of Stochastics at the Universität Ulm. Before pursuing his PhD, he earned an MSc in Mathematics from the Courant Institute of Mathematical Sciences, New York University, following dual undergraduate degrees in “Mathematics” and “Applied Mathematics” in Mexico.

Future Plans and MATH+ Research Highlights of Carlos Améndola

Améndola aims to establish himself as a research group leader, advancing innovative work in algebraic and geometric methods in data analysis. He plans to deepen his studies of MLE in specialized settings, such as the toric case, and continue exploring graphical models and their applications in data science. As part of the Collaborative Research Center (CRC) “Rough Analysis, Stochastic Dynamics and Related Fields” (SFB/Transregio 388), led by MATH+ Distinguished Fellow Peter K. Friz (TU Berlin), Améndola will contribute to interdisciplinary projects on stochastic systems and real-world applications.

MATH+ Research Highlights
Within MATH+, Améndola extends graphical models to analyze extreme values, with applications in rare events like natural disasters and financial market risks. For example, the models he researches are used to study flood dynamics, predicting water movement through networks during extreme weather, and to analyze stock market volatility, providing insights into rapid price changes.

LINKS: