Project
PaA-4
Free Flight Global Optimization via Eikonal Discretizations
Project Heads
Ralf Borndörfer, Martin Weiser
Project Members
Arturas Jocas
Project Duration
15.06.2024 − 31.12.2025
Located at
ZIB
Description
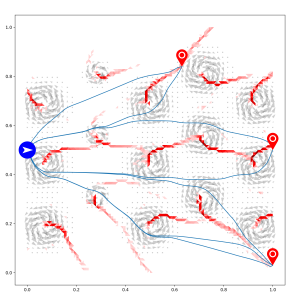
Optimal flight paths to three different destinations in a wind field consisting of many vortexes. Estimated cut loci are shown in red. Globally optimal paths to destinations positioned on cut loci are not unique.
Airlines demand globally optimal continuous flight paths in free flight areas under arbitrary wind conditions; this renders airway network based methods unfavorable. Building upon the successfully completed projects AA3-3 and TrU-4, we develop an eikonal discretization of the Hamilton-Jacobi-Bellman problem describing the continuous shortest path problem. The solution of the discretized problem produces globally optimal flight trajectories up to som discretization error. We investigate a priori error bounds, in particular for the position of cut loci, such that in most cases a single collocation-based optimal control solve starting at the approximate eikonal solution can be guaranteed to converges towards the globally optimal continuous trajectory.
Related Publications
- Arturas Jocas. Global Free Flight optimization by a Hamilton-Jacobi-Bellman approach. Master’s thesis, TU Berlin, 2024.

